ユークリッド原論をどう読むか(5)
頁末
前
次
目次
ユークリッド原論
第2巻
命題2ー2(全体とその分割部分との矩形)
「どちらかに」
もし
線分が
任意に2分されるならば、
全体と
分けられた部分のおのおのとに
かこまれた矩形の和は
全体の上の正方形に
等しい。
線分ABが
点Cにおいて任意に分けられたとせよ。
AB、BCにかこまれた矩形と
BA、ACにかこまれた矩形との
和は
AB上の正方形に等しい
と主張する。
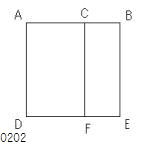
AB上に
正方形ADEBが描かれ、
Cを通り
AD、BEのどちらかに平行に
CFがひかれたとせよ。
- 命題1ー31による。
ADとBEは
定義1ー22により、
ABについて
同側内角の和が2直角であり、
命題1ー28により
平行である。
CFが
どちらに平行にひかれても、
命題1ー30により
他方とも平行である。
- 「どちらかに平行に」という表現は、
具体的な作図においては
どれか1つについて平行となるように
作業するという意味である。
以下、コメント(命題2ー2)(どちらかに)という。
そうすれば
[正方形]AEは
[矩形]AF、CEの和に等しい。
- 公理1ー7による。
- 矩形AFという表現は、
AとFが対角となっている矩形に用いる。
矩形DA、ACという表現と、
DA、ACにかこまれた矩形
という表現に区別はない。
また
矩形DA、ACと
矩形CA、ADとを
特に区別はしていない。
原論においては
裏返しも含めて
動かして重ねるという考え方が
根底にあるので、
このようになるのも当然である。
-
sq(AE)=rec(AF)+rec(CE)
[・・・・・・(1)]
そして
AEはAB上の正方形であり、
- 作図の設定である。
-
sq(AE)=sq(_AB)
[・・・・・・(2)]
AFは
BA、ACにかこまれた矩形である。
なぜなら
AFはDA、ACにかこまれ、
ADはABに等しいから。
また
CEは矩形AB、BCである。
なぜなら
BEはABに等しいから。
それゆえ
矩形BA、ACと
矩形AB、BCの和は
AB上の正方形に等しい。
よって
もし
線分が
任意に2分されるならば、
全体と
分けられた部分のおのおのとに
かこまれた矩形の和は
全体の上の正方形に等しい。
これが証明すべきことであった。
- 原典に示してある作図が
描かれた時点で
原典にある証明は
実質的に終わっている。
後は
長方形の面積を確認するだけであるから。
むしろ
証明された命題を前提として、
以後の命題を証明するというのが
原論の本来の精神ではなかろうか。
第2巻は、
いくぶん異なった趣である。
- 命題2ー1を前提とするなら、
次のように証明することもできる。
AB上の正方形は、
定義2ー1により矩形AB、ABである。
-
sq(_AB)=rec(AB、AB)
[・・・・・・(5)]
矩形AB、ABは、
命題2ー1により矩形AB、ACと
矩形AB、CBとの和に等しい。
-
rec(AB、AB)=rec(AB、AC)+rec(AB、CB)
[・・・・・・(6)]
よって、
AB上の正方形は、
公理1ー1により
矩形AB、ACと矩形AB、CBとの和に等しい。
- (5)
(6)
により AB^2=AB*AC+AB*CB
- 命題2-2は第2巻の命題によると次のようになる。
- 命題2-2は、
AB;線分
C;点(AB)
において、
rec(AB、AC)+rec(AB、CB)
=sq(_AB)
のことである。
- 命題2-2は推論用命題である。
前
次
目次
頁頭
