ユークリッド原論をどう読むか（８）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第４巻

命題４ー５（作図.三角形の外接円）
与えられた三角形に円を外接させること。

• 三角形は、 定義１ー１９の補足２ による。
• 円は、 定義１ー１５ による。
• 外接は、 定義４ー６ による。

与えられた
　三角形をＡＢＣとせよ。

• 　△ＡＢＣ
  をとっている。

与えられた
　三角形に
　円を外接させねばならぬ。

線分ＡＢ、ＡＣが
　点Ｄ、Ｅにおいて２等分され、

• 命題１ー１０ （作図・線分の２等分）
  による。
• 　中点Ｄ(ＡＢ)、
  　中点Ｅ(ＡＣ)
  をとっている。

　点Ｄ、Ｅから
　ＡＢ、ＡＣに直角に
　ＤＦ、ＥＦがひかれ【▲たとせよ。 【・・・(a)】

• 命題１ー１２ （作図・線分への垂線）
  により
  　ＤＦ、ＥＦ’がひかれる。
  命題１ー３１の補足２ (交線の垂線)
  により、
  　ＤＦ、ＥＦ’が１点で交わる。
  その点を改めてＦとし、
  　溯ってＦを用いている。
• 　交点Ｆ(垂線(Ｄ,ＡＢ),垂線(Ｅ,ＡＣ))
  をとっている。

すると
それらは
　三角形ＡＢＣの内部か
　線分ＢＣ上か
　または
　ＢＣの外部で
　相会するであろう。

• 場合分けである。
  ＦがＢＣ上にある場合、
  　ＦとＢ、Ｃとを結ぶ必要がないので、
  　この場合分けをおこなっている。
  ＦがＢＣ上にあっても、
  　ＦとＢ、Ｃとを結んでも差し支えない
  　と考えれば、
  　この場合分けは不要となる。 【・・・(Ca)】

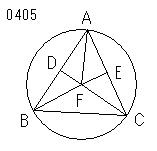
まず、
　内部で
　Ｆにおいて相会するとし▲】、

• 場合分けの第一である。
• 　Ｆ;内.△ＡＢＣ
  となっている。

　ＦＢ、ＦＣ、ＦＡが
　結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 　線分ＦＢ、ＦＣ、ＦＡ
  をとっている。

そうすれば、
ＡＤは
　ＤＢに等しく、

• (a) による。
• 　ＡＤ＝ＤＢ
  となっている。

ＤＦは
　共通でかつ直角をなすから、

• (a) による。
• 　ＤＦ＝ＤＦ
  　∠ＡＤＦ＝∠ＢＤＦ
  となっている。

底辺ＡＦは
　底辺ＦＢに等しい。

• 命題１ー４ （２辺挟角相等）
  による。
• 　ＡＦ＝ＦＢ
  となっている。

同様にして
　ＣＦがＡＦに等しいことも証明しうる。
それゆえ
　ＦＢもＦＣに等しい。

• 公理１ー１ （同じものに等しい）
  による。
• 　ＣＦ＝ＡＦ、
  　ＦＢ＝ＦＣ
  となっている。

ゆえに
　３線分ＦＡ、ＦＢ、ＦＣは
　互いに等しい。
したがって
　Ｆを中心とし、
　ＦＡ、ＦＢ、ＦＣの１つを半径として
　円が描かれれば、 【・・・(1)】

• 公準１ー３ （作図.円）
  による。
• 「〜の１つ」については、
  　コメント（命題４ー４）を参照のこと
  
• 「描かれれば」と
  　仮定形で表現している。
  命題４ー４ （作図.三角形の内接円）
  と同じ表現である。
• 　円(Ｆ,ＦＡ)
  をとっている。

　残りの点をも通り、

• 定義１ー１５ （円）
  による。
• 　Ｂ;上.円周(Ｆ,ＦＡ)
  　Ｃ;上.円周(Ｆ,ＦＡ)
  となっている。

　そして
この円は
　三角形ＡＢＣに外接されるであろう。

• 定義４ー６ （外接(円の)）
  による。
• 　円ＡＢＣ(Ｆ,ＦＡ);（外接）△ＡＢＣ
  となっている。

ＡＢＣのように外接されたとせよ。

• (1) の表現に対応している。
  命題４ー４ （作図.三角形の内接円）
  と同じである。

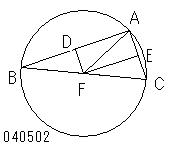
【▲ 次に
　第２図のように
　ＤＦ、ＥＦが
　線分ＢＣ上でＦにおいて相会するとし、

• 場合分けの第２である。
• (Ca) のコメントの後半にしたがえば、 　「次に」以下は不要である。
• 「第２図のように」という表現は
  　初めてである。
  これまでも
  　 命題３ー３３ （作図.与えられた角を含む切片）
  のように、
  　図が２つあった命題は存在した。
  しかし
  　それらの命題においても、
  　「第２図のように」という表現は
  　なかった。
  また、
  　最初の図については
  　「第１図のように」という
  　対応した表現がない
  　ことにも留意しておく。 【・・・(Cb)】
• 　Ｆ;上.ＢＣ
  となっている。　

　ＡＦが結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 　線分ＡＦ
  をとっている。

同様にして
点Ｆは
　三角形ＡＢＣに
　外接される円の中心である
　ことを証明しうる。

• ＦＡ、ＦＢ、ＦＣが相等しい
  　ことが全く同様に証明される。
• 　円(Ｆ,ＦＡ);（外接）△ＡＢＣ
  となっている。

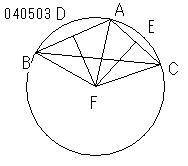
さらにまた
　第３図のように
　ＤＦ、ＥＦが
　三角形ＡＢＣの外部で
　Ｆにおいて相会するとし、

• 場合分けの第３である。
• 　Ｆ;外.△ＡＢＣ
  となっている。

　ＡＦ、ＢＦ、ＣＦが
　結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 　線分ＡＦ、ＢＦ、ＣＦ
  をとっている。

そうすればまた
ＡＤは
　ＤＢに等しく、

• (a) による。
• 　ＡＤ＝ＤＢ
  となっている。

ＤＦは
　共通でかつ直角をなすから、

• (a) による。
• 　ＤＦ＝ＤＦ、
  　ＤＦ⊥ＡＢ
  となっている。

底辺ＡＦは
　底辺ＢＦに等しい。

• 命題１ー４ （２辺挟角相等）
  による。
• 　ＡＦ＝ＢＦ
  となっている。

同様にして
　ＣＦがＡＦに等しい
　ことも証明しうる。
それゆえ
　ＢＦもＦＣに等しい。

• 公理１ー１ （同じものに等しい）
  による。
• 　ＣＦ＝ＡＦ、
  　ＢＦ＝ＦＣ
  となっている。

ゆえに
　Ｆを中心とし、
　ＦＡ、ＦＢ、ＦＣの１つを半径として
　円が描かれれば、

• 公準１ー３ （作図.円）
  による。
• 　円(Ｆ,ＦＡ)
  をとっている。

　残りの点をも通り、
　三角形ＡＢＣに
　外接されているであろう。▲】

• 定義１ー１５ （円）
  による。
• 第１の場合にある
  　「ＡＢＣのように
  　外接されたとせよ。」という
  　１文がないことに留意しておく。 【・・・(Cc)】
• 　Ｂ、Ｃ;上.円周(Ｆ,ＦＡ)、
  　円(Ｆ,ＦＡ);（外接）△ＡＢＣ
  となっている。

よって
　与えられた三角形に
　円が外接された。
　これが作図すべきものであった。
【▲そして
　次のことは明らかである、

• 「そして」以降は、
  　命題の本文にない部分である
  　ことに留意しておく。 【・・・(Cd)】

　すなわち
　円の中心が
　三角形の内部におちるときには、
角ＢＡＣは
　半円より大きい切片内にあるから、
　直角より小さく、

• 角ＢＡＣは、
  　切片ＢＡＣ内の角である。
  中心が
  　三角形ＢＡＣ内、
  　したがって
  　切片ＢＡＣ内
  　にあるから、
  　 公理１ー８ （大きい）
  により
  切片ＢＡＣは
  　半円より大きい。
  
• 命題３ー３１ （半円内の角は直角、半円より大小の切片内の角、切片の角）
  により、
  切片内の角（円周角）は
  　直角より小さい。
• 　Ｆ;内.△ＡＢＣ
  ならば、
  　切片ＢＡＣ.円ＡＢＣ;（含）半円.円ＡＢＣ、
  　内角ＡＢＣ.切片ＢＡＣ＜∠Ｒ
  となっている。

　中心が線分ＢＣ上におちるときには、
角ＢＡＣは
　半円内にあるから、
　直角である。

• 命題３ー３１ （半円内の角は直角、半円より大小の切片内の角、切片の角）
  による。
• 　Ｆ;辺ＢＣ.△ＡＢＣ
  ならば、
  　切片ＢＡＣ.円ＡＢＣ;半円.円ＡＢＣ
  　内角ＡＢＣ.切片ＢＡＣ＝∠Ｒ
  となっている。

また
　円の中心が
　三角形の外部におちるときには、
角ＢＡＣは
　半円より小さい切片内にあるから、
　直角より大きい。

• 角ＢＡＣは、
  　切片ＢＡＣ内の角である。
  中心が
  　三角形ＢＡＣの外、
  　したがって
  　切片ＢＡＣの外
  　にあるから、
  　 公理１ー８の補足 （小さい）
  により
  切片ＢＡＣは
  　半円より小さい。
  
• 命題３ー３１ （半円内の角は直角、半円より大小の切片内の角、切片の角）
  により、
  切片内の角（円周角）は
  　直角より大きい。
• 　Ｆ;外.△ＡＢＣ
  ならば、
  　切片ＢＡＣ.円ＡＢＣ;（含まれる）半円.円ＡＢＣ
  　内角ＡＢＣ.切片ＢＡＣ＞∠Ｒ
  となっている。▲】
• 原論における命題の証明の終わり方としては、
  　これまでのものとは
  　全く異なっている。
  命題にない、
  　余分なものまで
  　（それも、
  　半円より大きいかどうか
  　という同じテーマで）
  　論じているという点で
  　本命題とよく似ている
  　 命題３ー２５ （作図.切片から円を描く）
  と比べても、
  終わり方は
  　異なっている。
  また、
  　系をもっている 命題３ー１ （作図.円の中心）
  と比べても、
  　異なる終わり方をしている。 【・・・(Ce)】
• (Ca), (Cb), (Cc), (Cd), (Ce) により、
  　【▲　▲】で囲った部分は、
  　後世の解説が紛れ込んだものと思われる。

• 命題４ー５は、
  　△ＡＢＣ
  に対して、
  　中点Ｄ(ＡＢ)、
  　中点Ｅ(ＡＣ)、
  　交点Ｆ(垂線(Ｄ,ＡＢ),垂線(Ｅ,ＡＣ))
  をとれば、
  　円(Ｆ,ＦＡ);（外接）△ＡＢＣ
  のことである。
• 命題４ー５は作図用命題である。

  前提	作図	推論
  定義		1-15,4-6
  公準	1-1,1-3
  公理		1-1,1-8,1-8補
  命題	1-10,1-12,1-31補	1-4,3-31
  その他	コ(題4-4)

前 　　 次 　　 目次 　　頁頭