ユークリッド原論をどう読むか（２）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー９（作図・角の２等分）
　与えられた直線角を２等分すること。

• 直線角は定義１ー８による。
• ２等分は定義の補足（公理１ー６）による。

　与えられた直線角を
　角ＢＡＣ
とせよ。
このとき
　それを２等分し
なければならぬ。
　
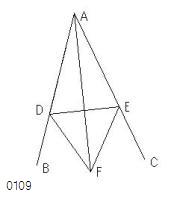
　ＡＢ上に任意の点Ｄが取られ、

• 　公準１ー１の補足（作図.任意の点をとる）
  による。
• 　点Ｄ(ＡＢ)
  をとっている。

　ＡＣから
　ＡＤに等しくＡＥが取られ、

• 　命題１ー３（作図・等しい線分を切り取る）
  による。
• 　点Ｅ(ＡＣ;;ＡＥ＝ＡＤ)
  をとっている。

　ＤＥが結ばれ、

• 　公準１ー１（作図.直線）
  による。
• 　線分(Ｄ,Ｅ)
  をとっている。

　ＤＥ上に
　等辺三角形ＤＥＦがつくられ、

• 　命題１ー１（作図・正三角形）
  による。
• 　点Ｆ(反対側(ＤＥ,Ａ);;△ＤＥＦ;等三(_ＤＥ))
  をとっている。

　ＡＦが結ばれた
とせよ。
　　　　　　【・・・(a)】

• 　公準１ー１（作図.直線）
  による。
• 　線分(Ａ,Ｆ)
  をとっている。

［そうすれば、］
　角ＢＡＣは
　線分ＡＦによって
　２等分されている
と主張する。

　ＡＤはＡＥに等しく、

• 　(a) による。
  
• 　ＡＤ＝ＡＥ
  となっている。

　ＡＦは共通である
から、
　２辺ＤＡ、ＡＦは
　２辺ＥＡ、ＡＦに
　それぞれ等しい。
そして
　底辺ＤＦは底辺ＥＦに等しい。

• 　前節、
  　(a)により、
  　ＤＥＦは等辺三角形による。
• 　(ＤＡ,ＡＦ)＝(ＥＡ,ＡＦ)、
  　ＤＦ＝ＥＦ
  となっている。

ゆえに
　角ＤＡＦは角ＥＡＦに等しい。

• 　前節、
  　命題１ー８（３辺相等２）
  による。
• 　∠ＤＡＦ＝∠ＥＡＦ
  となっている。

よって、
　与えられた角ＢＡＣは
　線分ＡＦによって２等分されている。
　これが作図すべきものであった。

• 命題1-9は、
  　∠ＢＡＣ
  に対して、
  　点Ｄ(ＡＢ)、
  　点Ｅ(ＡＣ;;ＡＥ＝ＡＤ)、
  　点Ｆ(反対側(ＤＥ,Ａ);;△ＤＥＦ;等三(_ＤＥ))
  をとるならば、
  　ＡＦ；２等分線（∠ＢＡＣ）
  のことである。　
  
• 命題1-9は作図用命題である。

  前提	作図	推論
  定義
  公準	1-1、1-1補
  公理
  命題	1-1、1-3	1-8
  その他

前 　　 次 　　 目次 　　頁頭