ユークリッド原論をどう読むか（５）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論

第２巻

命題２ー５（線分の矩形分割）
線分の矩形分割
もし
　線分が
　相等および不等な部分に分けられるならば、
　不等な［二つの］部分にかこまれた矩形と
　二つの区分点の間の線分上の正方形と
　の和は
　もとの線分の半分の上の正方形に等しい。

• 線分は、定義の補足（命題１−１）による。
• 相等、不等は、定義の補足（公理１−４）による。
• かこまれたは、定義２ー１による。
• 矩形は、定義１ー２２による。
• 正方形は、定義１ー２２による。
• 半分は、定義の補足（公理１ー６）による。
• 等しいは、公理１ー７による。
• 　線分
  に対して、
  　線分上の点で２つの線分に分割し、
  　一方の線分上に、
  　他の線分との矩形
  をとることを
  　線分の矩形分割という。
  (以下、定義の補足(命題２ー５)(線分の矩形分割)という。
  

任意の線分ＡＢが
　Ｃにおいて等しい［相等な］部分に、
　Ｄにおいて不等な部分に
　分けられたとせよ。

• 　線分ＡＢ、
  　中点Ｃ(ＡＢ)、
  　点Ｄ[ＡＢ]
  をとっている。

ＡＤ、ＤＢにかこまれた矩形と
　ＣＤ上の正方形と
　の和は
　ＣＢ上の正方形に等しい
　と主張する。

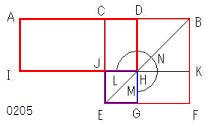
ＣＢ上に
　正方形ＣＥＦＢがえがかれ、

• 命題１−４６（作図.線分上に正方形）
  による。
• 　正方ＣＥＦＢ(_ＣＢ)
  をとっている。

ＢＥが結ばれ、

• 公準１−１（作図.直線）
  による。
• 　線分ＢＥ
  をとっている。

Ｄを通り
　ＣＥ、ＢＦのどちらかに平行に
　ＤＧがひかれ、

• 命題１−３１（作図・平行線）
  により一方に平行に引くと、
  　命題１−３０（平行の平行）
  により他方とも平行となる。
• 「どちらかに」については、
  　コメント（命題２ー２）を参照のこと
  
• ＢＥとＢＦは交わっており、
  　ＤＧとＢＦは平行だから、
  　命題１−３０の補足(交線に平行な線)
  により
  　ＢＥとＤＧは交わる。
  　その交点をＨとする。
  
• 　交点Ｇ(ＥＦ,平行線(Ｄ,ＢＦ))、
  　交点Ｈ(ＢＥ,ＤＧ)
  をとっている。

またＨを通り
　ＡＢ、ＥＦのどちらかに平行に
　ＩＫがひかれ、

• 命題１−３１（作図・平行線）
  により一方に平行に引くと、
  　命題１−３０（平行の平行）
  により他方とも平行となる。
• ＣＥ、ＢＦとＡＢは交わっており、
  　ＩＫとＡＢは平行だから、
  　命題１−３０の補足(交線に平行な線)
  により
  　ＣＥ、ＢＦとＩＫは交わる。
  　その交点をそれぞれＪ、（改めて）Ｋとする。
  　遡ってＫを用いている。
• 　交点Ｊ(ＣＥ,平行線(Ｈ,ＡＢ))、
  　交点Ｋ(ＢＦ,平行線(Ｈ,ＡＢ))
  をとっている。

さらに
　Ａを通り
　ＣＪ、ＢＫのどちらかに平行に
　ＡＩがひかれたとせよ。

• 命題１−３１（作図・平行線）
  により一方に平行に引くと、
  　命題１−３０（平行の平行）
  により他方とも平行となる。
• ＩＫとＢＫは交わっており、
  　ＡＩとＢＫは平行だから、
  　命題１−３０の補足(交線に平行な線)
  により
  　ＩＫとＡＩは交わる。
  　その交点を改めてＩとする。
  　遡ってＩを用いている。
• 　交点Ｉ(ＪＫ,平行線(Ａ,ＣＥ))
  をとっている。

そうすれば、
　補形ＣＨは補形ＨＦに等しいから、

• 命題１−４３（平行四辺形の補形）
  による。
• 補形については、
  　定義の補足（命題１ー４３）(対角線をはさむ平行四辺形・補形)
  による。
• 　矩形(ＣＨ)＝矩形(ＨＦ)
  　　　　　　【・・・(１)】

双方にＤＫが加えられたとせよ。
そうすれば
　ＣＫ全体はＤＦ全体に等しい。

• 公理１−２（等しいものに等しいものを加える）、
  　公理１−１の補足（等しいものに等しい）
  による。
• (1) より
  　矩形(ＣＨ)＋矩形(ＤＫ)
  　＝矩形(ＨＦ)＋矩形(ＤＫ)
  よって
  　矩形(ＣＫ)＝矩形(ＤＦ)
  　　　　　　【・・・(2)】

ところが、
　ＡＣはＣＢに等しいから、

• 作図の設定である。

ＣＫはＡＪに等しい。

• 定義２ー１（かこまれる）
  による。
• 　 　矩形(ＣＫ)＝矩形(ＡＪ)
  　　　　　　【・・・(3)】

ゆえに
　ＡＪもＤＦに等しい。

• 公理１−１の補足（等しいものに等しい）
  による。
• (2) (3) により
  　矩形(ＤＦ)＝矩形(ＡＪ)
  　　　　　　【・・・(4)】

双方にＣＨが加えられたとせよ。
そうすれば
　ＡＨ全体はグノーモーンＬＮＭに等しい。

• 公理１−２（等しいものに等しいものを加える）
  による。
• 定義２ー２（グノーモーン）
  による。
• 公理１ー１の補足（等しいものに等しい）
  による。
• (4) より
  　矩形(ＤＦ)＋矩形(ＣＨ)
  　＝矩形(ＡＪ)＋矩形(ＣＨ）
  　グ(ＬＮＭ)
  　＝矩形(ＤＦ)＋矩形(ＣＨ)
  よって
  　矩形(ＡＨ)＝グ(ＬＮＭ)
  　　　　　　　【・・・(5)】

ところが
　ＤＨは
　ＤＢに等しいから

• 命題２ー４の補足(正方形の対角線をはさむ正方形)
  による。
• 　ＤＨ＝ＤＢ
  となっている。

ＡＨは
　矩形ＡＤ、ＤＢである。

• 定義２ー１（かこまれる）
  による。
• 矩形(ＡＨ)＝矩形(ＡＤ、ＤＢ)
  　　　　　　【・・・(6)】

ＣＤ上の正方形に等しいＪＧが

• 命題２ー４の補足(正方形の対角線をはさむ正方形)
  による。
• 矩形(ＪＧ)＝正方(_ＣＤ)
  　　　　　　【・・・(7)】

双方に加えられたとせよ。
そうすれば
　グノーモーンＬＮＭとＪＧとの和は
　ＡＤ、ＤＢにかこまれた矩形と
　ＣＤ上の正方形と
　の和に等しい。

• 公理１−２（等しいものに等しいものを加える）
  による。
• (5) (6) (7) より
  　矩形(ＡＨ)+矩形(ＪＧ)
  　＝矩形(ＡＤ、ＤＢ)＋矩形(ＪＧ)
  よって
  　グ(ＬＮＭ)＋矩形(ＪＧ)
  　＝矩形(ＡＤ、ＤＢ)＋正方(_ＣＤ)
  　　　　　　【・・・(8)】

ところが
　グノモーンＬＮＭとＪＧとの和は
　ＣＢ上にある正方形ＣＥＦＢ全体に等しい。

• 公理１−７（等しい）
  による。
• 　グ(ＬＮＭ)＋矩形(ＪＧ)＝正方(_ＣＢ)
  　　　　　　【・・・(9)】

したがって
　ＡＤ、ＤＢにかこまれた矩形と
　ＣＤ上の正方形と
　の和は
　ＣＢ上の正方形に等しい。

• 公理１−１（同じものに等しい）
  による。
• (8) (9) より
  　矩形(ＡＤ、ＤＢ)＋正方(_ＣＤ)
  　＝正方(_ＣＢ)

よってもし
　線分が
　相等および不等な部分に分けられるならば、
　不等な［二つの］部分にかこまれた矩形と
　二つの区分点の間の線分上の正方形と
　の和は
　もとの線分の半分の上の正方形に等しい。
　
これが証明すべきことであった。

• 第２巻の命題によると、以下のような証明が可能である。
  矩形ＣＢ、ＢＤは
  　命題２−３（２分線分の全体と一つとによる矩形）
  により
  　矩形ＣＤ、ＢＤとＢＤ上の正方形との和
  　に等しい。
  
  • 　矩形(ＣＢ、ＢＤ)
    　＝矩形(ＣＤ、ＤＢ)＋正方(_ＢＤ)
    　　　　　　【・・・(10)】
  矩形ＡＣ、ＢＤは、
  　定義２−１（かこまれる）
  により
  　矩形ＣＢ、ＢＤである。
  
  • 　矩形(ＣＢ、ＢＤ)＝矩形(ＡＣ、ＢＤ)
    　　　　　　【・・・(11)】
  よって、
  　公理１ー１（同じものに等しい）
  により、
  　矩形ＡＣ、ＢＤは、
  　矩形ＣＤ、ＢＤとＢＤ上の正方形との和
  　に等しい。
  
  • (10) (11) により
    　矩形(ＣＤ、ＢＤ)＋正方(_ＢＤ)
    　＝矩形(ＡＣ、ＢＤ)
    　　　　　　【・・・(12)】
  双方に
  　ＣＤ上の正方形と矩形ＣＤ、ＢＤとの和を加えると、
  　公理１ー２（等しいものに等しいものを加える）
  により、
  　矩形ＡＣ、ＢＤとＣＤ上の正方形と矩形ＣＤ、ＢＤとの和は、
  　矩形ＣＤ、ＢＤの２倍とＢＤ上の正方形とＣＤ上の正方形との和に等しい。
  
  • (12) から
    　矩形(ＣＤ、ＢＤ)＋正方(_ＢＤ)
    　＋正方(_ＣＤ)＋矩形(ＣＤ、ＢＤ)
    　＝矩形(ＡＣ、ＢＤ)＋正方(_ＣＤ)＋矩形(ＣＤ、ＢＤ)
    　　　　　　【・・・(13)】
  • (13) から　定義の補足（公理１−５）（同じもののｎ倍）、
    　公理１−１（同じものに等しい）
    により
    　２×矩形(ＣＤ、ＢＤ)＋正方(_ＢＤ)＋正方(_ＣＤ)
    　＝矩形(ＡＣ、ＢＤ)＋正方(_ＣＤ)＋矩形(ＣＤ、ＢＤ)
    　　　　　　　【・・・(14)】
  矩形ＡＣ、ＢＤと矩形ＣＤ、ＢＤとの和は、
  　命題２−１（任意個分割との矩形）
  により、
  　矩形ＡＤ、ＢＤに等しいので、
  
  • 　矩形(ＡＣ、ＢＤ)＋矩形(ＣＤ、ＢＤ)＝矩形(ＡＤ、ＢＤ)
    　　　　　　　【・・・(15)】
  　矩形ＡＣ、ＢＤとＣＤ上の正方形と矩形ＣＤ、ＢＤとの和は、
  　公理１ー２（等しいものに等しいものを加える）
  により、
  　矩形ＡＤ、ＢＤとＣＤ上の正方形との和に等しい。
  
  • (15) から
    　矩形(ＡＣ、ＢＤ)＋正方(_ＣＤ)＋矩形(ＣＤ、ＢＤ)
    　＝矩形(ＡＤ、ＢＤ)＋正方(_ＣＤ)
    　　　　　　【・・・(16)】
  矩形ＣＤ、ＢＤの２倍とＢＤ上の正方形とＣＤ上の正方形との和は、
  　命題２−４（２分線分上の正方形）
  により、
  　ＣＢ上の正方形に等しい。
  
  • 　２×矩形(ＣＤ、ＢＤ)＋正方(_ＢＤ)＋正方(_ＣＤ)
    　＝正方(_ＣＢ)
    　【・・・(17)】
  よって、
  　矩形ＡＤ、ＢＤとＣＤ上の正方形との和は、
  　公理１ー１の補足（等しいものに等しい）
  により、
  　ＣＢ上の正方形に等しい。
  
  • (16) (14) (17) から
    　矩形(ＡＤ、ＢＤ)＋正方(_ＣＤ)
    　＝正方(_ＣＢ)
    
  • 命題2-5は第２巻の命題によると次のようになる。

    前提	作図	推論
    定義		補(理1-5),2-1
    公準
    公理		1-1,1-1補,1-2
    命題		2-1,2-3,2-4
    その他

• 命題2-5は、
  本質的には、和と差の積は平方の差である。
  　Ｘ＝ＡＢ／２、Ｙ＝ＣＤ
  とおくと、
  　矩形(Ｘ＋Ｙ、ＸーＹ)＝正方(_Ｘ)ー正方(_Ｙ)
  
• 　和ＡＣ＋ＣＢと積ＡＣ×ＣＢの値
  を既知として、
  　ＡＣとＣＢ
  を求める方法、
  つまり、
  　今日的にいう２次方程式の解の公式
  を図形的に示している。
  すなわち、
  　Ｚ；正方(_Ｚ)＝正方(_和／２)ー積
  をとると、
  　ＡＣ＝和／２＋Ｚ、
  　ＣＢ＝和／２ーＺ
  として求められる。
• 命題2-5は、
  　ＡＢ；線分
  に対して、
  　Ｃ；点[ＡＢ;;中点でない]、
  　Ｄ；中点(ＡＢ)
  をとるならば、
  　正方(_ＡＤ)＝正方(_ＣＤ)＋矩形(ＡＣ,ＣＢ)
  のことである。
  
• 命題2-5は推論用命題である。

• 前提	作図	推論
  定義		2-1,2-2
  公準	1-1
  公理		1-1,1-1補,1-2,1-7
  命題	1-30補,1-31,1-46	1-30,1-43,2-4補
  その他	どちらかに

  
  

前 　　 次 　　 目次 　　頁頭