ユークリッド原論をどう読むか(5)
頁末
前
次
目次
ユークリッド原論
第2巻
命題2ー3(2分線分の全体と一つとによる矩形)
もし
線分が
任意に2分されるならば、
全体と一つの部分とにかこまれた矩形は
二つの部分にかこまれた矩形と
先にいわれた部分の上の正方形との
和に等しい。
線分ABが
Cにおいて
任意に分けられたとせよ。
AB、BCにかこまれた矩形は
AC、CBにかこまれた矩形と
BC上の正方形との和に等しいと主張する。
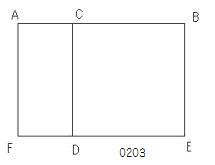
CB上に
正方形CDEBが描かれ、
- 命題1ー46(作図.線分上に正方形)
による。
-
正方CDEB(_CB)
をとっている。
EDが
Fまで延長され、
- 公準1ー2(作図.直線の延長)
による。
-
点F'[延長ED]
をとっている。
Aを通り
CD、BEのどちらかに平行に
AFがひかれたとせよ。
- 命題1ー31(作図・平行線)
による。
命題1ー30(平行の平行)
により
どちらに平行にひかれても
他方とも平行である。
- 「どちらかに」については、
コメント(命題2ー2)を参照のこと
- CDとEFは交わっており、
CDとAGが平行であるように
AGをひくと、
命題1ー30の補足(交線に平行な線)
により
EFとAGは交わる。
この交点を溯ってFとしている。
原論ではこのような推論を省略している場面が多い。
-
交点F(EF',平行線(A,CD))
をとっている。
そうすれば
AEはAD、CEの和に等しい。
- 公理1ー7(等しい)
による。
-
矩形(AE)
=矩形(AD)+矩形(CE)
[・・・・・・(6)]
そして
AEは
AB、BCにかこまれた矩形である。
なぜなら
それは
AB、BEにかこまれており、
BEはBCに等しいから。
また
ADは矩形AC、CBである。
なぜなら
DCはCBに等しいから。
そして
DB[CE]は
CB上の正方形である。
- 作図の設定である。
-
矩形(CE)=正方(_CB)
[・・・・・・(4)]
それゆえ
AB、BCにかこまれた矩形は
AC、CBにかこまれた矩形と
BC上の正方形と
の和に等しい。
よって
もし
線分が
任意に2分されるならば、
全体と一つの部分とにかこまれた矩形は
二つの部分にかこまれた矩形と
先にいわれた部分の上の正方形と
の和に等しい。
これが証明すべきことであった。
- 命題2ー1により
次のように証明される。
矩形AB、BCは、
命題2ー1(任意個分割との矩形)
により
矩形BC、ACとBC、CBの和に等しい。
-
矩形(AB、BC)=矩形(BC、AC)+矩形(BC、CB)
[・・・・・・(5)]
矩形BC、CBは、
定義2ー1(かこまれる)
によりBC上の正方形である。
-
矩形(BC、CB)=正方(_BC)
[・・・・・・(6)]
よって、
矩形AB、BCは
公理1ー2(等しいものに等しいものを加える)、
公理1ー1(同じものに等しい)
により
矩形AC、BCとBC上の正方形と
の和に等しい。
- (5)
(6)
により
矩形(AB、BC)=矩形(AC、BC)+正方(_BC)
となっている。
- 命題2-3は第2巻の命題によると次のようになる。
- 命題2-3は、
AB;線分、
C;点[AB]
において、
矩形(AB、BC)=矩形(AC、CB)+正方(_BC)
のことである。
- 命題2-3は推論用命題である。
前
次
目次
頁頭
