ユークリッド原論をどう読むか(14)
頁末
前
次
目次
ユークリッド原論
第10巻
命題10ー79(余線分に付加して全体と平方のみ通約となる有理線分は唯一)
余線分には
それに付加されて
全体と平方においてのみ通約
できる
ただ一つの有理線分が
ある。
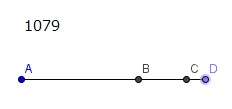
ABを
余線分
とし、
BCが
それに
付加された
とせよ。
そうすれば
AC、CBは
平方においてのみ通約
できる
有理線分である.
ABには
全体と
平方においてのみ通約
できる
他のいかなる線分も
付加されない
と主張する。
もし可能ならば、
BDが
付加された
とせよ。
)]
そうすれば
AD、DBは
平方においてのみ通約
できる
有理線分である。
-
背理法の仮定である。
-
AD∩^^2 DB
AD、DB;有理線分
となっている。
そして
AD、DB上の正方形の和と
矩形AD、DBの2倍との
差は
AC、CB上の正方形の和と
矩形AC、CBの2倍との差に
等しい。
なぜなら
その差は
共に同じAB上の正方形
である
から。
-
命題2ー7(差の平方)
による。
-
「なぜなら」は、
コメント2(命題1ー16)
参照のこと。
-
正方(_AD)+正方(_DB)ー2矩形(AD、DB)
=正方(_AB)
=正方(_AC)+正方(_CB)ー2矩形(AC、CB)
となっている。
したがって
いれかえて
AD、DB上の正方形の和と
AC、CB上の正方形の和との
差は
矩形AD、DBの2倍と
矩形AC、CBの2倍との差に
等しい。
-
前節による。
-
正方(_AD)+正方(_DB)ー正方(_AC)+正方(_CB)
=2矩形(AD、DB)ー2矩形(AC、CB)
となっている。
ところが
AD、DB上の正方形の和と
AC、CB上の正方形の和との
差は
有理面積
である。
なぜなら
両方とも
有理面積
である
から。
したがって
矩形AD、DBの2倍は
矩形AC、CBの2倍より
有理面積だけ
大きい。
-
前節による。
なお、
DB>CBを
前提としている。
DB<CB
ならば、
「大きい」を
「小さい」とすればよい。
-
矩形(AD、DB)ー矩形(AC、CB);有理面積
となっている。
これは不可能である。
なぜなら
両方とも
中項面積
であり、
中項面積と
中項面積の
差が
有理面積
であることはない
から。
したがって
ABには
全体と平方においてのみ通約
できる
他のいかなる有理線分も
付加されない。
よって
余線分には
それに
付加されて
全体と平方においてのみ通約
できる
ただ一つの有理線分が
ある。
-
前節による。
-
AC;有理線分、
BC;有理線分、∩^^2 AC
AB;余線分
となる有理線分は唯一
となっている。
これが証明すべきことであった。
- 命題10ー79は、
命題の補足2(定義10ー3)(作図.任意の有理線分)、
命題10ー6の系3(作図.長さ・平方で通約可の線分)
命題1ー3(作図・等しい線分を切り取る)
により
AC;有理線分、
BC;有理線分、∩^^2 AC
AB;余線分
をとり、
BD;有理線分、
AD;有理線分、
となるなら、
BD=BC
のことである。
- 命題10ー79は推論用命題である。
前
次
目次
頁頭
