ユークリッド原論をどう読むか（１６）
頁末 　　 前 　　 次 　 目次

ユークリッド原論

第１１巻
　
命題１１ー６（同一平面に垂直な２直線は平行）
もし
　２直線が
　　　同一平面に対し
　　垂直である
ならば，
　それらの２直線は
　　平行であろう。

• 直線は、
  定義１ー４による。
• 平面は、
  定義１ー７による。
• 垂直は、
  定義１１ー３の補足による。
• 平行は、
  定義１ー２３による。

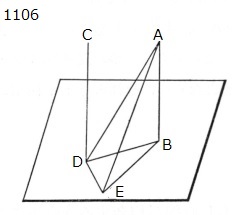
　２直線ＡＢ,ＣＤが
　　基準平面に垂直である
とせよ。

• 　公準１ー１の補足（作図.任意の点をとる）
  により、
  　基準平面上に、点Ｂ、Ｄ
  をとる。
  　公準１ー１の補足２（作図.任意の線分）
  により、
  　線分ＢＤ
  をとり、
  　公準１ー１の補足（作図.任意の点をとる）
  により、
  　直線ＢＤ上にない点Ｚ
  をとり、
  　公準１ー１の補足２（作図.任意の線分）
  により、
  　ＺとＢ、Ｄをそれぞれ結ぶ。
  　命題１１ー４の補足(作図.交わる２直線の交点を通る、２直線に垂直な直線)
  により、
  　ＢＺ、ＢＤに垂直なＡＢ
  をとり、
  　ＤＺ、ＤＢに垂直なＣＤ
  をとる。
  
• 　ＡＢ、ＣＤ⊥基準平面
  となっている。

　ＡＢは
　　ＣＤに平行である
と主張する。

　　基準平面と点Ｂ,Ｄで交わる
とし，

• 　前節
  による。
• 　ＡＢ、ＣＤ⊥基準平面、
  　Ｂ、Ｄ；基準平面上
  となっている。　

　線分ＢＤが
　　結ばれ，
　　　ＢＤに垂直に
　　　基準平面上に
　ＤＥが
　　ひかれ，
　ＤＥが
　　ＡＢに等しくされ，
　ＢＥ,ＡＥ,ＡＤが
　　結ばれた
とせよ。
　　　　[......(１)]

• 　公準１ー１（作図.直線）、
  　命題１ー１１（作図・線分からの垂線）、
  　命題１ー３の補足（作図.等しい線分となる点）、
  　公準１ー１（作図.直線）
  による。
• 　線分ＢＤ、
  　線分ＤＥ（基準平面上；ＤＥ⊥ＢＤ、ＤＥ＝ＡＢ）、
  　線分ＢＥ、ＡＥ、ＡＤ
  となっている。　

そうすれば
　ＡＢは
　　基準平面に垂直である
から，
　　それと会し
　　かつ
　　基準平面上にある
　　　すベての線分に対しても
　直角をなす。

• 　命題の設定、
  　定義１１ー３（直角(直線・平面)）
  による。

ところが
　ＢＤ,ＢＥの双方は
　　基準平面上にあり
　　ＡＢと会する。

• 　命題の設定、 （１）
  による。　
• 　ＢＤ、ＢＥ；基準平面上、（交わる）ＡＢ
  となっている。

それゆえ
　角ＡＢＤ, ＡＢＥの双方は
　　直角である。

• 　前節、
  　定義１１ー３（直角(直線・平面)）
  による。
• 　∠ＡＢＤ、∠ＡＢＥ＝∠Ｒ
  となっている。

同じ理由で
　角ＣＤＢ,ＣＤＥの双方も
　　直角である。

• 　命題の設定、 （１）、
  　定義１１ー３（直角(直線・平面)）
  による。
• 　∠ＣＤＢ、∠ＣＤＥ＝∠Ｒ
  となっている。

そして
　ＡＢは
　　ＤＥに等しく，
　ＢＤは
　　共通である

• 　（１）
  による。
• 　ＡＢ＝ＤＥ、
  　ＢＤ；共通
  となっている。

から，
　２辺ＡＢ,ＢＤは
　　２辺ＥＤ,ＤＢに等しい。
そして
　　直角をはさむ。

• 　前節、前々節による。
• 　（ＡＢ、ＢＤ）＝（ＥＤ、ＤＢ）、
  　∠ＡＢＤ＝∠ＥＤＢ
  となっている。

ゆえに
　底辺ＡＤは
　　底辺ＢＥに等しい。

• 　前節、
  　命題１ー４（２辺挟角相等）
  による。
• 　ＡＤ＝ＢＥ

そして
　ＡＢは
　　ＤＥに，
　他方ＡＤも
　　ＢＥに等しい

• 　前節、 （１）
  による。
• 　ＡＢ＝ＤＥ、
  　ＡＤ＝ＢＥ
  となっている。

から，
　２辺ＡＢ,ＢＥは
　　２辺ＥＤ,ＤＡに等しい。
そして
　ＡＥは
　　それらの共通な底辺である。

• 　前節による。
• 　（ＡＢ、ＢＥ）＝（ＥＤ、ＤＡ）、
  　ＡＥ；共通
  となっている。

したがって
　角ＡＢＥは
　　角ＥＤＡに等しい。

• 　前節、
  　命題１ー８の補足（３辺相等による合同）
  による。
• 　∠ＡＢＥ＝∠ＥＤＡ
  となっている。

そして
　角ＡＢＥは
　　直角である。

• 　命題の設定
  による。
• 　∠ＡＢＥ＝∠Ｒ
  となっている。

それゆえ
　角ＥＤＡも
　　直角である。

• 　前節、前々節
  　公理１ー１（同じものに等しい） による。
• 　∠ＥＤＡ＝∠Ｒ
  となっている。

ゆえに
　ＥＤは
　　ＤＡに垂直である。

• 　前節
  による。
• 　∠ＥＤＡ＝∠Ｒ
  となっている。

ところが
　　　ＢＤ,ＤＣの双方に対しても
　　垂直である。

• 　命題の設定
  　定義１１ー３（直角(直線・平面)）
  による。
• 　ＥＤ⊥ＢＤ、ＤＣ
  となっている。

したがって
　ＥＤは
　　　３線分ＢＤ,ＤＡ,ＤＣに対し
　　交点において垂直に立てられた。

• 　前節、前々節
  による。
• 　ＥＤ⊥ＢＤ、ＤＡ、ＤＣ
  となっている。

それゆえ
　３線分ＢＤ,ＤＡ,ＤＣは
　　一平面上にある。

• 　前節、
  　命題１１ー５（交わる３直線に垂直な直線があれば、３直線は同一）
  による。
• 　ＢＤ、ＤＡ、ＤＣ；同一平面上

ところが
　ＤＢ,ＤＡが
　　いかなる平面上にあろうと，
　ＡＢも
　　同じ平面上にある。
なぜなら
　すべての三角形は
　　一平面上にあるから。

• 　命題１１ー２（交わる２直線、三角形は同一平面上）
  による。
• 　ＤＢ、ＤＡ、ＡＢ；同一平面上
  となっている。

ゆえに
　線分ＡＢ,ＢＤ,ＤＣは
　　一平面上にある。

• 　前節、前々節
  による。
• 　ＡＢ、ＢＤ、ＤＣ；同一平面上

そして
　角ＡＢＤ,ＢＤＣの双方は
　　直角である。

• 　命題の設定、
  　定義１１ー３（直角(直線・平面)）
  による。
• 　∠ＡＢＤ、∠ＢＤＣ＝∠Ｒ
  となっている。

したがって
　ＡＢは
　　ＣＤに平行である。

• 　前節、
  　定義１ー２３（平行(線)）
  　命題１ー２８（内対角、同側内角と平行）
  による。
• 　ＡＢ‖ＣＤ
  となっている。

よって
もし
　２直線が
　　同一平面に対し垂直である
ならば，
　それらの２直線は
　　平行であろう。

• 　前節による。

これが証明すべきことであった。

• 命題１１ー６は、
  もし
  　２直線が
  　　同一平面に対し垂直である
  ならば，
  　　２直線と基準平面との交点２点を結び、
  　　　結んだ直線と一方の直線とに対する
  　　垂線を基準平面にとり、
  　　　直線と垂線の交点と、
  　　他方の直線上の点を結ぶ
  ことにより、
  　２直線が
  　　同一平面上であるとわかり、
  　それらの２直線は平行
  のことである。
• 命題１１ー６は推論用命題である。

  前提	作図・構成	推論
  定義		1-23,11-3
  公準	1-1,1-1補,1-1補2
  公理		1-1
  命題	1-3補,1-11,11-4補	1-4,1-8補,1-28,11-2,11-5
  その他

前 　　 次 　　 目次 　　頁頭