ユークリッド原論をどう読むか（１６）
頁末 　　 前 　　 次 　 目次

ユークリッド原論

第１１巻
　
命題１１ー７（平行直線上の点を結ぶと同一平面上）
(作図.空間に平行線)
もし
　２直線が
　　平行であり，
　　　それらの双方の上に
　任意の点が
　　とられる
ならば，
　それらの点を結ぶ直線は
　　平行線と同じ平面上にある。

• 直線は、
  定義１ー４による。
• 平行は、
  定義１ー２３による。
• 点は、
  定義１ー１による。
• 平面は、
  定義１ー７による。

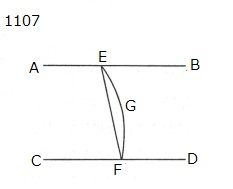
　　　ＡＢ,ＣＤを
　　二つの平行線とし，
　　　それらの双方の上に
　任意の点Ｅ,Ｆが
　　とられたとせよ。

• 　公準１ー１の補足２（作図.任意の線分・直線をひく）
  により、
  　任意の直線ＡＢをとり、
  　公準１ー１の補足（作図.任意の点をとる）
  により、
  　ＡＢ外に点Ｃをとり、
  　命題１１ー２の補足(作図.交わる２直線、１直線上にない３点、１直線とその上にない１点で平面が決定)
  により、
  　平面ＡＢＣをとり、
  　命題１ー３１（作図・平行線）
  により、
  　　　ＡＢ上に、
  　Ｃをとおり、ＡＢに平行な直線ＣＤをとる。
  以上により、
  　空間に２本の平行線をとることができる。
  (以下、命題１１ー７の補足(作図.空間に平行線)という。)
  　公準１ー１の補足（作図.任意の点をとる）
  により、
  　ＡＢ上にＥを、
  　ＣＤ上にＦをとる。
• 　ＡＢ‖ＣＤ
  　Ｅ（ＡＢ；）、
  　Ｆ（ＣＤ；）
  となっている。

　　点Ｅ,Ｆを結ぶ

• 　公準１ー１（作図.直線）
  による。
• 　ＥＦ（Ｅ、Ｆ；）
  となっている。

　直線は
　　平行線と同じ平面上にある
と主張する。
そうでない
ならば，

• 　背理法の仮定を述べようとしている。

もし
可能ならば，
　　　ＥＧＦのように
　　平面外にある
とし，
　　ＥＧＦを通り
　平面が
　　つくられた
とせよ。

• 背理法の仮定として、
  　ＥＦが平面上にない
  とすると、
  　Ｇ（ＥＦ；平面外）
  がとられる。
  　公準１ー１の補足（作図.任意の点をとる）
  により、
  　　ＥＦ上にない点Ｚをとると、
  　命題１１ー２の補足(作図.交わる２直線、１直線上にない３点、１直線とその上にない１点で平面が決定)
  により、
  　　平面をとる。
• 　平面（ＥＧＦ、Ｚ；）
  となっている。
  以下の推論では、
  　　この平面を基準平面とする。

そうすれば
　　　基準平面上に交線として
　　線分をつくるであろう.
　　ＥＦのようにつくるとせよ。

• 　前節、
  　命題１１ー３（２平面の交線は直線）
  による。
• 　交線ＥＦ（ＡＢＣ、ＥＦＺ；）
  となっている。

そうすれば
　２線分ＥＧＦ,ＥＦは
　　面積をかこむであろう。

• 　前節、 背理法の仮定、
  による。
  
• 　交線ＥＦ、線分ＥＧＦ；平面ＥＦＺ上、
  　Ｇ；交線ＥＦ外
  となっている。

これは不可能である。

• 　公理１ー９（２点を通る直線は一致）
  による。

ゆえに
　Ｅ,Ｆを結ぶ線分は
　　平行線ＡＢ,ＣＤを通る平面上にある。

• 　前節、 　背理法
  による。
• 　線分ＥＦ；平面（ＡＢ、ＣＤ；）
  となっている。

よって
もし
　２直線が
　　平行であり，
　　　それらの双方の上に
　任意の点が
　　とられる
ならば，
　　それらの点を結ぶ
　直線は
　　平行線と同じ平面上にある。
これが証明すべきことであった。

• 命題１１ー７は、
  　ＡＢ‖ＣＤ、
  　Ｅ（ＡＢ；）、
  　Ｆ（ＡＢ；）
  のとき、
  　ＥＦ、ＡＢ、ＣＤ；同一平面上
  のことである。
  
• 命題１１ー７は推論用命題である。

  前提	作図・構成	推論
  定義
  公準
  公理
  命題
  その他	コ6(題5-1)

前 　　 次 　　 目次 　　頁頭