ユークリッド原論をどう読むか(3)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1ー28(内対角、同側内角と平行)
外角・内対角(平行線)
もし
1直線が2直線に交わってなす
一つの外角が
同じ側の内対角に等しいか
または
同側内角の和が2直角に等しければ、
この2直線は互いに平行であろう。
- 直線は、定義1ー4による。
- 交わるは、定義1ー8の補足による。
- 外角、内対角は、
通常、
定義の補足(命題1ー16)によるが、
登場する3直線のうち2直線が平行である場合、
外角は、
無限遠に第三の頂点がある
三角形ができているものとみなして、
平行線の外側の角をいい、
内対角は
その外角と共通となる辺(直線)について
同じ側にある、
平行線の内側の角をいう。
(以下、定義の補足(命題1ー28)(外角・内対角(平行線))という。)
- 同じ側にあるとは定義1ー7の補足による。
- 等しいは、公理1ー7による。
- 内角は、定義の補足(公準1ー5)による。
- 直角は、定義1ー10による。
- 平行は、定義1ー23による。
- 外角と同じ側の内対角とのことを
今日では同位角といっている。
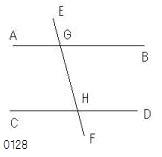
2直線AB、CDに
直線EFが交わってなす
外角EGBが
内対角GHDに等しいか
または同側内角BGH、GHDの和が
2直角に等しいとせよ。
-
直線AB
に対して、
点G[AB]、
点H[外.AB]、
点E[延長HG]、
点D[同側(GH,B);;∠GHD=∠EGB]、
または
点D[同側(GH,B);;∠GHD+∠BGH=2×∠R]、
点C[延長DH]
をとっている。
ABはCDに平行であると主張する。
角EGBは角GHDに等しく、
- 命題の設定
による。
-
∠EGB=∠GHD
となっている。
また
角EGBは角AGHに等しいから、
- 命題1ー15(対頂角)
による。
-
∠EGB=∠AGH
となっている。
角AGHもGHDに等しい。
- 公理1ー1(同じものに等しい)
による。
-
∠AGH=∠GHD
となっている。
そして
錯角である。
それゆえ
ABはCDに平行である。
- 命題1ー27(錯角と平行)
による。
-
AB‖CD
となっている。
また
角BGH、GHDの和は2直角に等しく、
- 命題の設定
による。
-
∠BGH=∠GHD
となっている。
角AGH、BGHの和も2直角に等しいから、
- 命題1ー13(直線と2直角1)
による。
-
∠AGH+∠BGH=2×∠R
となっている。
角AGH、BGHの和は
角BGH、GHDの和に等しい。
- 公理1ー1(同じものに等しい)
による。
-
∠AGH+∠BGH=∠BGH+∠GHD
となっている。
双方から
角BGHが引きさられたとせよ。
そうすれば
残りの角AGHは残りの角GHDに等しい。
- 公理1ー3(等しいものから等しいものをひく)
による。
-
∠AGH=∠GHD
となっている。
しかも錯角である。
ゆえにABはCDに平行である。
- 命題1ー27(錯角と平行)
による。
AB‖CD
となっている。
よってもし
1直線が
2直線に交わってなす
一つの外角が
同じ側の内対角に等しいか
または
同側内角の和が
2直角に等しければ、
この2直線は互いに平行であろう。
これが証明すべきことであった。
- この命題は
公準1ー5(平行線公準)
の裏である。
- 命題1ー27(錯角と平行)
を前提とせず、
命題1ー17(三角形の2角の和)
を前提として証明することができる。
そして、
この命題を前提として
命題1ー27(錯角と平行)
を証明することができる。
したがって、
命題1ー27(錯角と平行)、
命題1ー28(内対角、同側内角と平行)
は同値である。
- 命題1ー27(錯角と平行)、
命題1ー28(内対角、同側内角と平行)
により、
公準1ー5(平行線公準)
を前提とせずに、
任意の直線に対して
錯角が等しい
(あるいはこれに同等な)
平行線が存在することが、
命題1ー31(作図・平行線)
で証明される。
- 命題1-28は、
直線AB、CD、EF
に対して、
交点G(直線EF,直線AB)、
交点H(直線EF,直線CD)、
とするとき
外角EGB=内対角GHD
または
同側内角∠BGH+∠GHD=2×∠R
ならば、
AB‖CD
のことである。
- 命題1-28は推論用命題である。
前
次
目次
頁頭
