ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第１０巻
　
命題１０ー２（互除で常に余るなら非通約）
もし
　２つの不等な量のうち、
　つぎつぎに
　小さいほうが大きいほうからひかれ、
　残された量が
　けっして
　自分の前の量を割り切ることがない
ならば、
　それらの２量は通約できない
であろう。

• 不等は、
  定義の補足（公理１ー４）による。
• 量は、
  定義５ー１の補足による。
• 小さいは、
  公理１ー８の補足による。
• 大きいは、
  公理１ー８による。
• 割り切るは、
  定義５ー１の補足２による。
• 通約は、
  定義１０ー１による。

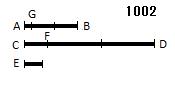
　２つの不等な量ＡＢ、ＣＤがあり、
　そのうち
　ＡＢが小さく、
　つぎつぎに
　小さいほうが大きいほうからひかれ、

• 　「量（について）・・・とせよ」は、
  　コメント６（命題５ー１）
  　参照のこと。
  
• 　命題１ー３（作図.等しい線分を切り取る）
  による。
  

　残された量が
　けっして
　自分の前の量を割り切ることがない
とせよ。

　量ＡＢ、ＣＤは通約できない
と主張する。

もし
　通約できる
ならば、

• 　背理法の仮定を述べようとしている。

　何らかの量が
　それらを割り切る
であろう。

• 　定義１０ー１（通約）
  による。
  

もし可能ならば

• 　「もし可能ならば」は、
  　コメント２(命題１−７）
  　参照のこと。
  

　割り切る
とし、
　それをＥ
とせよ。

• 　背理法の仮定である。
• 　Ｅ｜ＡＢ、Ｅ｜ＣＤ
  としている。

　ＡＢがＦＤを割り切り、
　自分より小さいＣＦを残す
とし、
　　　　　　[......(ａ)]

• 　ＡＢ｜ＦＤ、
  　ＡＢ＞ＣＦ
  となっている。

　ＣＦがＢＧを割り切り、
　自分より小さいＡＧを残す
とし、
　　　　　　[......(ｂ)]

• 　ＣＦ｜ＢＧ、
  　ＣＦ＞ＡＧ
  となっている。
  

そして
　これがたえずくりかえされ、
　Ｅより小さい何らかの量が残される
までせよ。

• 　命題１０ー１（繰り返し半分以下でいくらでも小さくなる）
  による。
  

そうなったとし、
　Ｅより小さいＡＧが残された
とせよ。
　　　　　　[......(Ｃ)]

• 　準一般的な証明である。
  　コメント２（命題５ー１）
  　参照のこと。
  
• 　Ｅ＞ＡＧ
  となっている。

そうすれば
　ＥはＡＢを割り切り、

• 　背理法の仮定による。
• 　Ｅ｜ＡＢ
  となっている。

　他方
　ＡＢはＤＦを割り切る

• 　（ａ）による。
• 　ＡＢ｜ＤＦ
  となっている。

から、
　ＥはＦＤをも割り切る
であろう。

• 　前節、前々節、
  　命題５ー３の補足（倍量の倍量は倍量）
  による。
  
• 　Ｅ｜ＦＤ
  となっている。

そして
　ＥはＣＤ全体を割り切る。

• 　背理法の仮定による。
• 　Ｅ｜ＣＤ
  となっている。

したがって
　残りのＣＦをも割り切る
であろう。

• 　前節、前々節、
  　命題５ー６の補足（倍量の差は倍量）
  による。
  
• 　Ｅ｜ＣＦ
  となっている。

ところが
　ＣＦはＢＧを割り切る。

• 　（ｂ）による。

それゆえ
　ＥはＢＧをも割り切る。

• 　前節、前々節、
  　命題５ー３の補足（倍量の倍量は倍量）
  による。
  による。
  
• 　Ｅ｜ＢＧ
  となっている。

そして
　ＡＢ全体をも割り切る。

• 　背理法の仮定による。
• 　Ｅ｜ＡＢ
  となっている。

したがって
　残りのＡＧをも割り切る
であろう、

• 　前節、前々節、
  　命題５ー６の補足（倍量の差は倍量）
  による。
  
• 　Ｅ｜ＡＧ
  となっている。

すなわち
　大きい量が
　小さい量を割り切る
であろう。

• 　前節、
  　（ｃ）による。

　これは不可能である。

• 　定義５ー１の補足２（割り切る）
  による。

したがって
　いかなる量も
　量ＡＢ、ＣＤを割り切らない
であろう。

• 　背理法による。

ゆえに
　量ＡＢ、ＣＤは通約できない。

• 　定義１０ー１（通約）
  による。

よってもし
　２つの不等な量のうち云々

これが証明すべきことであった。

• 云々は、
  「小さいほうが大きいほうからひかれ、
  　残された量が
  　けっして
  　自分の前の量を割り切ることがない
  ならば、
  　それらの２量は通約できない
  であろう。」
  である。
  
  
• 　命題７ー１（互除法１）における
  　いわゆる
  　ユークリッドの互除法は
  　２数における共通な尺度
  　すなわち
  　公約数を求めるものであった
  ということができる。
  
  
• 命題１０ー２は、
  任意のｍについて、
  　Ａm＝Ｑm×Ｂm＋Ａm+1、
  　Ｂm＝Ｑ'm×Ａm+1＋Ｂm+1、
  　Ｂm＞Ａm+1＞０、
  　Ａm+1＞Ｂm+1＞０
  ならば、
  　Ａ1¬∩Ｂ1
  ということである。
  
  
• 命題１０ー２は推論用命題である。

  前提	作図	推論
  定義		5-1補2,10-1
  公準
  公理
  命題	1-3	5-3補,5-6補,10-1
  その他	コ6(題5-1)	コ2(題1-7),コ2(題5-1)

前 　　 次 　　 目次 　　頁頭