ユークリッド原論をどう読むか（９506）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー６（同数倍の差２）
（倍量の差は倍量）
もし
　２つの量が
　　２つの量の同数倍であり、
　前者から引き去られる２量が
　　後者の同数倍であるならば、
　残りの２量は
　同じ後者に等しいか
　または
　それらの同数倍である。

• 量は、定義５ー１の補足 による。
• 同数倍は、定義５ー５の補足 による。
• 等しいは、公理１ー７ による。
• この命題では
  　同数倍と等しいを区別している。
  すなわち、
  　原論では
  　等しいを１倍と同一視していない。
  つまり、
  　１（単位）を数とは見ていない。
  　命題５ー２ では、
  　加えているので
  　基準となる量に
  　等しくなる場合はないので、
  　区別していない。
  

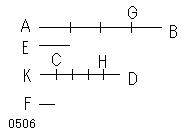
２つの量ＡＢ、ＣＤが
　２つの量Ｅ、Ｆの同数倍であるとし、
　引き去られる量ＡＧ、ＣＨが
　同じＥ、Ｆの同数倍とせよ。
残りのＧＢ、ＨＤは
　Ｅ、Ｆに等しいか
　または
　それらの同数倍であると主張する。
　

• 量の倍は、命題の補足（定義５ー２）（作図.倍量）、
  量の差は、命題の補足（定義５ー１５）（作図.量の和）
  による。
• 　ＡＢ＝ｍＥ、
  　ＣＤ＝ｍＦ、
  　ＡＧ＝ｎＥ、
  　ＣＨ＝ｎＦ
  をとっている。

　［ＧＢについて、
　Ｅに等しい場合、
　Ｅの何倍かに等しい場合
がある。］
まず、
　ＧＢがＥに等しいとせよ。
【・・・(a)】

• ＧＢがＥに等しい場合を
  　証明しようとしている。
• 　ＧＢ＝Ｅ
  となっている。

ＨＤも
　Ｆに等しいと主張する。

ＣＫをＦに等しくせよ。 【・・・(b)】

• 推論の設定である。
• 　ＣＫ＝Ｆ
  をとっている。

ＡＧはＥの、
　ＣＨはＦの同数倍であり、

• 命題の設定による。
• 　ＡＧ＝ｎＥ、
  　ＣＨ＝ｎＦ
  となっている。

　ＧＢはＥに、
　ＫＣはＦに等しいから、

• (a)(b) による。
• 　ＧＢ＝Ｅ、
  　ＫＣ＝Ｆ
  となっている。

　ＡＢはＥの、
　ＫＨはＦの同数倍である。【・・・(1)】

• 命題５ー２（同数倍の和２）
  による。
• 　個数(ＡＢ,Ｅ)＝個数(ＫＨ,Ｆ)＝ｎ＋１
  となっている。

ところが
　ＡＢはＥの、
　ＣＤはＦの同数倍である
　ことが仮定されている。

• 命題の設定による。
• 　ＡＢ＝ｍＥ、
  　ＣＤ＝ｍＦ
  となっている。

それゆえ
　ＫＨはＦの、
　ＣＤはＦの同数倍である。

• (1)、公理の補足３（命題５ー１）(１対１対応)
  による。
• 　個数(ＫＨ,Ｆ)＝個数(ＣＤ,Ｆ)＝ｍ＝ｎ＋１
  となっている。

そこで
　ＫＨ、ＣＤの双方は
　Ｆの同数倍であるから、
　ＫＨはＣＤに等しい。

• 定義５ー５の補足（同数倍） 、
  公理１ー５の補足２（等しいもののｎ倍、ｎ倍に等しいもの）
  による。
• 　ＫＨ＝ＣＤ＝ｍ＝ｎ＋１
  となっている。

双方から
　ＣＨがひかれたとせよ。
そうすれば
　残りのＫＣは
　残りのＨＤに等しい。

• 公理１ー３（等しいものから等しいものをひく）
  による。
• 　ＫＣ＝ＨＤ
  となっている。

しかも
　ＦはＫＣに等しい。

• (b) による。
• 　Ｆ＝ＫＣ
  となっている。

したがって
　ＨＤはＦに等しい。

• 公理１ー１（同じものに等しい）
  による。
• 　ＨＤ＝Ｆ
  となっている。

ゆえにもし
　ＧＢがＥに等しければ、
　ＨＤもＦに等しいであろう。

• (a) による。
• 　ＧＢ＝Ｅ
  ならば、
  　ＨＤ＝Ｆ
  となっている。

［　ＧＢがＥの何倍かの場合、］
同様にしてもし
　ＧＢがＥの何倍かであれば、
　ＨＤもＦの《同じ倍数》［同数倍］である
　ことを証明しうる。

• 推論の設定として、
  　ＣＫをＦの、
  　ＧＢがＥの何倍かと
  　　同数倍にすればよい。
  
• 　ＧＢ＝ｐＥ
  ならば、
  　点Ｋ(延長ＤＣ;;個数(ＣＫ,Ｆ)＝個数(ＧＢ,Ｅ))
  をとると、
  　ＧＢ＝ｐＥ、
  　ＫＣ＝ｐＦ、
  　ＡＢ＝ｍＥ＝(ｎ＋ｐ)Ｅ、
  　ＫＨ＝(ｎ＋ｐ)Ｆ、
  　ＣＤ＝ｍＦ
  となり、
  　ＫＨ＝ＣＤ＝ｍＦ＝(ｎ＋ｐ)Ｆ
  となるので、
  　ＣＨ＝ｎＦ
  をひくと、
  　ＫＣ＝ＨＤ＝ｐＦ
  となっている。
  

［ 以上の２つの場合から、］
よってもし
　２つの量が
　　２つの量の同数倍であり、
　前者から引き去られる２量が
　　後者の同数倍であるならば、
　残りの２量は
　　同じ後者に等しいか
　または
　　それらの同数倍である。
［これが証明すべきことであった。］

• したがって、
  　本命題と、
  　定義５ー２ （倍量）
  により、
  　 小さい量（基準とする大きさ）が何であろうと、
  　それについて
  　任意の倍量と別の任意の倍量との差は、
  　個数の差となる量で、
  　倍量であるか等しい。
  （以下、命題５ー６の補足（倍量の差は倍量）という。）
  
• 命題５ー６の補足は、
  ｍＣーｎＣ＝（ｍーｎ）Ｃのことである。
• 命題５ー６は、
  　個数(ｍＣーｎＣ,Ｃ)＝個数(ｍＦーｎＦ,Ｆ)
  のことである。
  
• 命題５ー６の補足（倍量の差は倍量）

  前提	作図	推論
  定義		5-2
  公準
  公理
  命題		5-6
  その他

• 命題５ー６は推論用命題である。

  前提	作図	推論
  定義		5-5補
  公準
  公理		1-1,1-3,1-5補2,補3(題5-1)
  命題	補(義5-2), 補(義5-15)	5-2
  その他		場合分け

前 　　 次 　　 目次 　　頁頭