ユークリッド原論をどう読むか（９503）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー３（同数倍の同数倍）
（倍量の倍量は倍量）
もし
　第１の量が第２の、
　第３が第４の
　　同数倍であり、
　第１と第３の同数倍が
　とられるならば、
　等間隔比により、
　とられた量のうち
　前者は第２の、
　後者は第４の
　それぞれ同数倍であろう。

• 量は、定義５ー１の補足 による。
• 同数倍は、定義５ー５の補足 による。
• 等間隔比は、定義５ー１７ による。
  ただし、
  　ここの
  　等間隔比により
  とは、
  　２つの量の列(Ｂ、Ａ、ＥＦとＤ、Ｃ、ＧＨ)それぞれで、
  　等間隔の項（第１項と第３項）に注目すると
  という意味であって、
  　推論の根拠として等間隔比
  をとりあげているのではない。
  　原論特有の言い回し
  である。
  

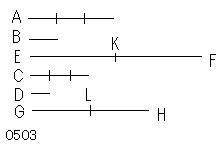
第１の量Ａは
　第２のＢの、
　第３のＣは
　第４のＤの
　　同数倍とし、
　Ａ、Ｃの同数倍ＥＦ、ＧＨが
　とられたとせよ。

• 量の倍は、
  命題の補足（定義５ー２）（作図.倍量）
  による。
• 　Ａ＝ｍＢ、
  　Ｃ＝ｍＤ、
  　ＥＦ＝ｎＡ、
  　ＧＨ＝ｎＣ
  をとっている。

ＥＦはＢの、
　ＧＨはＤの
　同数倍であると主張する。

ＥＦはＡの、
　ＧＨはＣの
　同数倍であるから、

• 命題の設定による。
• 　ＥＦ＝ｎＡ、
  　ＧＨ＝ｎＣ
  となっている。

　ＥＦのなかにある
　　Ａに等しい量と同数の、
　　Ｃに等しい量が
　ＧＨのなかにある。 【・・・(1)】

• 定義５ー５の補足（同数倍）
  による。
• 　個数(ＥＦ,Ａ)＝個数(ＧＨ,Ｃ)＝ｎ
  となっている。

ＥＦが
　Ａに等しい量ＥＫ、
　[ＫiＫ'i、]ＫＦに、
　ＧＨが
　Ｃに等しい量ＧＬ、
　[ＬiＬ'i、]ＬＨに
　分けられたとせよ。【・・・(a)】

• 　コメント２（命題５ー１）、
  　コメント５（命題５ー１）
  を参照のこと。
• 　ＥＦ＝ΣＫiＫ'i、
  　ＧＨ＝ΣＬiＬ'i
  となっている。

そうすれば
　ＥＫ、[ＫiＫ'i、]ＫＦの個数は
　ＧＬ、[ＬiＬ'i、]ＬＨの個数に
　等しいであろう。

• (1) による。
• 　個数(ＫiＫ'i)
  　＝個数(ＬiＬ'i)
  　＝ｎ
  となっている。

そして
　ＡはＢの、
　ＣはＤの
　同数倍であり、

• 命題の設定 による。
• 　Ａ＝ｍＢ、
  　Ｃ＝ｍＤ
  となっている。

　ＥＫはＡに、
　ＧＬはＣに
　等しいから、

• (a) による。
• 　ＥＫ＝Ａ、
  　ＧＬ＝Ｃ
  となっている。

　ＥＫはＢの、
　ＧＬはＤの
　同数倍である。【・・・(2)】

• 公理１ー１（同じものに等しい） 、
  定義５ー５の補足（同数倍）
  による。
• 　ＥＫ＝ｍＢ
  　ＧＬ＝ｍＤ
  となっている。

同じ理由で
　[ＫiＫ'iはＢの、]
　[ＬiＬ'iはＤの]
　ＫＦはＢの、
　ＬＨはＤの
　同数倍である。

• 　KiK'i＝ｍＢ、
  　LiL'i＝ｍＤ、
  　ＫＦ＝ｍＢ、
  　ＬＨ＝ｍＤ
  となっている。

そこで
　《第１》［第５の１］のＥＫは第２のＢの、
　《第３》［第６の１］のＧＬは第４のＤの
　同数倍であり、

• (2) による。
• 　倍数(ＥＫ,Ｂ)＝倍数(ＧＬ,Ｄ)＝ｍ
  となっている。

　［第５のKiK'iは第２のＢの、］
　［第６のLiL'iは第４のＤの、］
　第５のＫＦは
　第２のＢの、
　第６のＬＨは
　第４のＤの
　同数倍であるから、

• 　倍数(ＫiＫ'i,Ｂ)＝倍数(ＬiＬ'i,Ｄ)＝ｍ
  　倍数(ＫＦ,Ｂ)＝倍数(ＬＨ,Ｄ)＝ｍ
  となっている。

　《第１》［第５のＥＫ］《と》
　[、KiK'i、]
　第５［のＫＦ］の和ＥＦは
　　第２のＢの、
　《第３》［第６のＧＬ］《と》
　[、LiL'i、]
　第６［のＬＨ］の和ＧＨは
　　第４のＤの
　同数倍である。

• 公理の補足３（命題５ー１）(１対１対応) 、
  定義５ー５の補足（同数倍）
  による。
• 　倍数(ΣＫiＫ'i,Ｂ)
  　＝倍数(ΣＬiＬ'i,Ｄ)
  　＝ｎｍ
  となっている。
  

よってもし
　第１の量が第２の、
　第３が第４の
　同数倍であり、
　第１と第３の同数倍が
　とられるならば、
　等間隔比により、
　とられた量のうち
　　前者は第２の、
　　後者は第４の
　それぞれ同数倍であろう。
これが証明すべきことであった。

• 命題５ー３は、
  　倍数(ｎ(ｍＢ),Ｂ)＝倍数(ｎ(ｍＤ),Ｄ)＝ｎｍ、
  すなわち、
  　ｎ(ｍＢ)＝ｎｍＢ のことである。
  したがって
  　本命題と
  　定義５ー２（倍量）
  により、
  　 小さい量（基準とする大きさ）が何であろうと、
  　それについて
  　倍量の倍量は、
  　もとの倍量である。
  （以下、命題５ー３の補足（倍量の倍量は倍量）という。）
  
• 命題５ー３の補足（倍量の倍量は倍量）

  前提	作図	推論
  定義		5-2
  公準
  公理
  命題		5-3
  その他

• 命題５ー３は推論用命題である。

  前提	作図	推論
  定義		5-5補
  公準
  公理		1-1,補3(題5-1)
  命題	補(義5-2)
  その他		コ2(題5-1), コ5(題5-1)

前 　　 次 　　 目次 　　頁頭