ユークリッド原論をどう読むか(14)
頁末
前
次
目次
ユークリッド原論
第10巻
命題10ー1(繰り返し半分以下でいくらでも小さくなる)
2つの不等な量が定められ、
もし
大きいほうの量から
その半分より大きい量がひかれ、
残りから
また
その半分より大きい量がひかれ、
これがたえずくりかえされる
ならば、
最初に定められた小さいほうの量よりも
小さい何らかの量が残されるに至る
であろう。
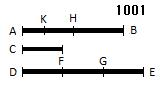
AB、Cを2つの不等な量
とし、
そのうちABが大きい
とせよ。
もし
ABから
その半分より大きい量がひかれ、
残りから
また
その半分より大きい量がひかれ、
-
命題1ー3(作図.等しい線分を切り取る)
による。
これがたえずくりかえされる
と、
量Cより小さい何らかの量が
残されるにいたる
であろうと主張する。
Cは何倍かされて
いつか
ABより大きくなる
であろう。
倍された
とし、
DEがCの倍量で、
ABより大きい
とし、
[......(a)]
-
前節により、
数mがあって、
DE=m×C
DE>AB
となっている。
また
DEが
Cに等しいDF、FG、GEに
分けられた
とし、
[......(b)]
-
準一般的な証明である。
コメント2(命題5ー1)
参照のこと。
-
m=3の場合を
可能な限り
一般的に論じている。
-
DF=FG=GE=C
となっている。
そして
ABから
その半分より大きいBHが、
AHから
その半分より大きいHKがひかれ、
これがたえずくりかえされ、
ABが
DEと等しい個数に分けられる
までせよ。
[......(c)]
そこで
AK、KH、HBが
DF、FG、GEと等しい個数に
分けられたもの
とせよ。
-
AB=AK+HK+BH、
DE=DF+FG+GE
と、
同じ個数に分けられている。
そうすれば
DEはABより大きく、
DEから
その半分より小さいEGが、
ABから
その半分より大きいBHがひかれている
から、
残りのGDは残りのHAより大きい。
[......(d)]
-
前節、前々節
公理1ー8の補足6(半分より大きい、小さい)
により、
DG>DE/2、AB/2>HA
となっており
公理1ー8の補足4(大きい・小さいもののn倍・n等分)
により、
DE/2>AB/2
となっているので、
公理1ー8の補足3(大きい・小さいものより大きい・小さい)
による。
-
GD>HA
となっている。
そして
GDはHAより大きく、
GDからその半分GFが、
HAからその半分より大きいHKがひかれている
から、
残りのDFは残りのAKより大きい。
-
前節
公理1ー8の補足6(半分より大きい、小さい)
により、
DF=GD/2、HA/2>AK
となっており
公理1ー8の補足4(大きい・小さいもののn倍・n等分)
により、
DG/2>HA/2
となっているので、
公理1ー8の補足3(大きい・小さいものより大きい・小さい)
による。
-
DF>AK
となっている。
そして
DFはCに等しい。
それゆえ
CはAKより大きい。
-
前節、前々節、
公理1ー8の補足2(等しいものより大きい・小さい) という)
による。
-
C>AK
となっている。
したがって
AKはCより小さい。
よって
最初に定められた
小さいほうの量Cより
小さい量AKが
量ABから残されている。
これが証明すべきことであった。
そして
もし
ひかれる部分が半分であっても、
同様にして証明されうる。
-
(a)において、
DEがCの3倍以上であれば、
(d)が成立するので、
同様に不等号が成立する。
-
命題7ー31(合成数を割り切る素数の存在)
の証明において、
原論の本文を補足した部分と
本質的に同じ内容
である。
-
命題10ー1は、
Bm>Am/2、
Am+1=AmーBm
とすると、
任意のCに対して、
あるnがあって、
An<C
ということである。
- 命題10ー1は推論用命題である。
前
次
目次
頁頭
