ユークリッド原論をどう読むか（１２）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第８巻
　
命題８ー１９（相似な立体数と２比例中項数）
（構成.相似な立体数の２比例中項数）)
　２つの相似な立体数の間には
　２つの比例中項数が入る。

そして
　立体数は
　相似な立体数に対し
　対応する辺が対応する辺に対する
　比の３乗の比をもつ。

• 相似は、
  定義７ー２２による。
• 立体数は、
  定義７ー１８による。
• 比例中項は、
  定義の補足３（命題６ー８）による。
• 数は、
  定義７ー２による。
• 対するは、
  定義の補足３（命題５ー１１）による。
• 辺は、
  定義７ー１８の補足による。
• 比は、
  定義５ー３による。
• ３乗の比は、
  定義５ー１０による。

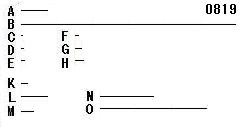
　Ａ、Ｂを２つの相似な立体数
とし、
　Ｃ、Ｄ、ＥをＡの、
　Ｆ、Ｇ、ＨをＢの辺
とせよ。

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
  
• 　Ｃ×Ｄ×Ｅ＝Ａ、Ｆ×Ｇ×Ｈ＝Ｂ
  となっている。

そうすれば
　相似な立体数は
　比例する辺をもつ
から、
　ＣがＤに対するように、
　ＦがＧに対し、
　ＦがＧに対するように、
　ＧがＨに対する。

• 　前節、
  　定義７ー２２
  により、
  　Ｃ：Ｄ＝Ｆ：Ｇ＝Ｇ：Ｈ
  となっている。
  

　Ａ、Ｂの間には
　２つの比例中項数が入り、
　ＡはＢに対し、
　ＣがＦに、
　ＤがＧに、
　さらに
　ＧがＨに対する比の
　３乗の比をもつ
と主張する。

　ＣがＤにかけてＫをつくり、
　ＦがＧにかけてＬをつくる
とせよ。
　　　　　　[......(ａ)]

• 　Ｃ×Ｄ＝Ｋ、Ｆ×Ｇ＝Ｌ
  となっている。

そうすれば
　Ｃ、ＤはＦ、Ｇと同じ比をなし、
　ＫはＣ、Ｄの積、
　ＬはＦ、Ｇの積である

• 　命題の設定、 前節
  による。

から、
　ｋ、Ｌは相似な平面数である。

• 　前節、
  　定義７−２２（相似な平面数・立体数）
  による。
• 　Ｃ×Ｄ＝Ｋ、Ｆ×Ｇ＝Ｌ
  　Ｃ：Ｄ＝Ｆ：Ｇ
  となっている。

それゆえ
　Ｋ、Ｌの間には
　１つの比例中項数がある。

• 　前節、
  　命題８ー１８（相似な平面数と比例中項）
  による。

　それをＭ
とせよ。
　　　　　　[......(１)]

• 　前節、前々節により、
  　Ｋ：Ｍ＝Ｍ：Ｌ
  となっている。

そうすれば
　前の定理で証明されたように、
　ＭはＤ、Ｆの積である。

• 　「前の定理で」という参照は
  　原論では異例である。
  　後世の注釈と考えられる。
  
• 　前々節、前々々節、
  　命題８ー１８（相似な平面数と比例中項）
  により、
  　Ｄ×Ｆ＝Ｍ
  となっている。

そして
　ＤがＣにかけてＫをつくり、
　ＦにかけてＭをつくった

• 　（ａ）、前節による。　
• 　Ｄ×Ｃ＝Ｋ、Ｄ×Ｆ＝Ｍ
  となっている。

から、
　ＣがＦに対するように
　ＫがＭに対する。

• 　前節、
  命題７ー１７（同数を各項にかけても比は同じ）
  による。
• 　Ｃ：Ｆ＝Ｋ：Ｍ
  となっている。

ところが
　ＫがＭに対するように、
　ＭがＬに対する。

• 　（１）による。
• 　Ｋ：Ｍ＝Ｍ：Ｌ
  となっている。

したがって
　Ｋ、Ｍ、Ｌは
　Ｃ対Ｆの比をなして
　順次に比例する。
　　　　　　[......(２)]

• 　前節、前々節による。

そして
　ＣがＤに対するように、
　ＦがＧに対する

• 　命題の設定による。

から、
　いれかえて
　ＣがＦに対するように、
　ＤがＧに対する。

• 　前節、
  　命題７ー１３（比例４数はいれかえても比例）
  による。

同じ理由で
　ＤがＧに対するように、
　ＥがＨに対する。

それゆえ
　Ｋ、Ｍ、Ｌは
　Ｃ対Ｆ、Ｄ対Ｇ、Ｅ対Ｈの比をなして
　順次に比例する。
　　　　　　[......(３)]

• 　（２）、前節、前々節、
  　命題５ー１１（同一の比に同じ比）
  による。
  
• 　Ｋ：Ｍ＝Ｍ：Ｌ、
  　Ｋ：Ｍ＝Ｃ：Ｆ＝Ｄ：Ｇ＝Ｅ：Ｈ
  となっている。
  

次に
　Ｅ、ＨはＭにかけて
　それぞれＮ、Ｏをつくる
とせよ。
　　　　　　[......(ｂ)]

• 　Ｅ×Ｍ＝Ｎ、Ｈ×Ｍ＝Ｏ
  となっている。
  

そうすれば
　Ａは立体数であり、
　Ｃ、Ｄ、Ｅはその辺である

• 　命題の設定による。

から、
　ＥはＣ、Ｄの積にかけてＡをつくった。

• 　前節による。
• 　Ｅ×Ｃ×Ｄ＝Ａ
  となっている。

ところが
　Ｃ、Ｄの積はＫである。

• 　（ａ）による。

ゆえに
　ＥはＫにかけてＡをつくった。
　　　　　　[......(４)]

• 　前節、前々節、
  　公理の補足５（定義７ー１６）（等を等にかけると等）
  による。
  
• 　Ｅ×Ｋ＝Ａ
  となっている。

同じ理由で
　ＨもＬにかけてＢをつくった。
　　　　　　[......(５)]

• 　命題の設定、 （ａ）
  により、
  　Ｈ×Ｆ×Ｇ＝Ｂ、Ｆ×Ｇ＝Ｌ
  となっていて、
  　公理の補足５（定義７ー１６）（等を等にかけると等）
  による。
  
• 　Ｈ×Ｌ＝Ｂ
  となっている。　

そして
　ＥはＫにかけてＡをつくり、
　ＭにかけてＮをつくった

• （４）、 （ｂ）による。
• 　Ｅ×Ｋ＝Ａ、Ｅ×Ｍ＝Ｎ
  となっている。

から、
　ＫがＭに対するように、
　ＡがＮに対する。

• 　前節、
  　命題７ー１７（同数を各項にかけても比は同じ） による。
• 　Ｋ：Ｍ＝Ａ：Ｎ
  となっている。

ところが
　ＫがＭに対するように、
　ＣがＦに、
　ＤがＧに、
　さらに
　ＥがＨに対する。

• 　（３）による。　

したがって
　ＣがＦに対するように、
　ＤもＧに、
　ＥもＨに、
　ＡもＮに対する。
　　　　　　[......(６)]

• 　前節、前々節
  　命題５ー１１（同一の比に同じ比）
  による。
  

また
　Ｅ、ＨはＭにかけて
　それぞれＮ、Ｏをつくった

• 　（ｂ）による。
• 　Ｅ×Ｍ＝Ｎ、Ｈ×Ｍ＝Ｏ
  となっている。

から、
　ＥがＨに対するように、
　ＮもＯに対する。

• 　前節、
  　命題７ー１７（同数を各項にかけても比は同じ） による。
• 　Ｅ：Ｈ＝Ｎ：Ｏ
  となっている。

ところが
　ＥがＨに対するように、
　ＣがＦに、
　ＤがＧに対する。

• 　（６）による。

それゆえ
　ＣがＦに対するように、
　ＤがＧに、
　ＥがＨに、
　ＡがＮに、
　ＮがＯに対する。
　　　　　　[......(７)]

• 　前節、前々節、 （６） 　命題５ー１１（同一の比に同じ比）
  による。
  
• 　Ｃ：Ｆ＝Ｄ：Ｇ＝Ｅ：Ｈ＝
  　Ａ：Ｎ＝Ｎ：Ｏ
  となっている。

また
　ＨはＭにかけてＯをつくり、
　他方
　ＬにかけてＢをつくった

• 　（ｂ）、 （５）による。
• 　Ｈ×Ｍ＝Ｏ、Ｈ×Ｌ＝Ｂ
  となっている。

から、
　ＭがＬに対するように、
　ＯがＢに対する。

• 　前節、
  　命題７ー１７（同数を各項にかけても比は同じ） による。
• 　Ｍ：Ｌ＝Ｏ：Ｂ
  となっている。

ところが
　ＭがＬに対するように、
　ＣがＦに、
　ＤがＧに、
　ＥがＨに対する。

• 　（３）による。

ゆえに
　ＣがＦに、
　ＤがＧに、
　ＥがＨに対するように、
　ＯがＢ対する
だけでなく、
　ＡもＮに、
　ＮもＯに対する。

• 　前節、 （７）、
  　命題５ー１１（同一の比に同じ比）
  による。
  
• 　Ｃ：Ｆ＝Ｄ：Ｇ＝Ｅ：Ｈ＝Ｏ：Ｂ＝
  　Ａ：Ｎ＝Ｎ：Ｏ
  となっている。

したがって
　Ａ、Ｎ、Ｏ、Ｂは
　上述の辺の比をなして
　順次に比例する。
　　　　　　[......(８)]

• 　前節、
  　定義の補足（命題８ー１）（順次に比例）
  による。
  

　Ａはまた
　Ｂに対し
　対応する辺が対応する辺に対する比、
　すなわち
　数ＣがＦに、
　ＤがＧに、
　ＥがＨに対する比の
　３乗の比をもつ
と主張する。

　Ａ、Ｎ、Ｏ、Ｂは
　４つの順次に比例する数である

• 　（８）による。

から、
　ＡはＢに対し、
　ＡがＮに対する比の
　３乗の比をもつ。

• 　前節、
  　定義５ー１０（３乗の比）
  による。
  

ところが
　ＡがＮに対するように、
　ＣがＦに、
　ＤがＧに、
　さらに
　ＥがＨに対する
ことが先に証明された。

• 　（７）による。

それゆえ
　ＡはＢに対し、
　対応する辺が対応する辺に対する比、
　すなわち
　数ＣがＦに、
　ＤがＧに、
　さらに
　ＥがＨに対する比の
　３乗の比をもつ。

• 　前節、前々節、
  　命題５ー１１（同一の比に同じ比）
  による。

　これが証明すべきことであった。

• 命題８ー１９は
  　Ａ＝Ｃ×Ｄ×Ｅ、
  　Ｂ＝Ｆ×Ｇ×Ｈ、
  　Ｃ：Ｆ＝Ｄ：Ｇ＝Ｅ：Ｈ
  ならば、
  　Ａ、Ｂの間に２つの比例中項数が入り、
  　Ａ：Ｃ×Ｇ×Ｅ
  　＝Ｃ×Ｇ×Ｅ：Ｃ×Ｇ×Ｈ
  　＝Ｃ×Ｇ×Ｈ：Ｂ
  かつ
  　Ａ：Ｂ＝（Ｃ：Ｆ）^3
  のことである。
  　証明の過程から、
  　次のことがわかる。
  　相似な立体数において、
  　対応しない２組の辺の積を
  　残りの１組の辺にかけた積の２数が
  　２つの比例中項
  となる。
  (以下、命題８ー１９の補足 （構成.相似な立体数の２比例中項数）という)
  　すなわち、
  　Ａ＝Ｃ×Ｄ×Ｅ、Ｂ＝Ｆ×Ｇ×Ｈ、
  　Ｃ：Ｄ：Ｅ＝Ｆ：Ｇ：Ｈ
  とすると、
  　Ａ：Ｃ×Ｇ×Ｅ
  　＝Ｃ×Ｇ×Ｅ：Ｃ×Ｇ×Ｈ
  　＝Ｃ×Ｇ×Ｈ：Ｂ
  となっている。
• 命題８ー１８の補足 （構成.相似な平面数の比例中項数）

  前提	作図	推論
  定義
  公準
  公理
  命題		8-19
  その他

• 命題８ー１９は推論用命題である。

  前提	作図	推論
  定義		5-10,7-22,補(題8-1)
  公準
  公理		補5(義7-16)
  命題		5-11,7-13,7-17,8-18
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭