ユークリッド原論をどう読むか（１２）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第８巻
　
命題８ー１８（相似な平面数と比例中項数）
（構成.相似な平面数の比例中項数）)
　２つの相似な平面数の間には
　１つの比例中項数がある。

そして
　平面数は平面数に対し
　対応する辺が
　対応する辺に対する比の
　２乗の比をもつ。

• 相似は、
  定義７ー２２による。
• 平面数は、
  定義７ー１７による。
• 比例中項は、
  定義の補足３（命題６ー８）による。
• 数は、
  定義７ー２による。
• 対するは、
  定義の補足３（命題５ー１１）による。
• 辺は、
  定義７ー１７の補足による。
• 比は、
  定義５ー３による。
• ２乗の比は、
  定義５ー９による。

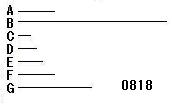
　２つの相似な平面数をＡ、Ｂ
とし、
　数Ｃ、ＤをＡの、
　Ｅ、ＦをＢの辺
とせよ。

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
  
• 　Ｃ×Ｄ＝Ａ、Ｅ×Ｆ＝Ｂ
  となっている。

そうすれば
　相似な平面数は
　比例する辺をもつ

• 　定義７−２２（相似な平面数・立体数）
  による。

から、
　ＣがＤに対するように、
　ＥがＦに対する。

• 　Ｃ：Ｄ＝Ｅ：Ｆ
  となっている。

そこで
　Ａ、Ｂの間には
　１つの比例中項数があり、
そして
　ＡはＢに対し、
　ＣがＥに
　または
　ＤがＦに対する比、
　すなわち
　対応する辺が
　対応する辺に対する比の
　２乗の比をもつ
と主張する。

そこで
　ＣがＤに対するように、
　ＥがＦに対する

• 　命題の設定である。

から、
　いれかえて
　ＣがＥに対するように、
　ＤがＦに対する。
　　　　　　[......(１)]

• 　命題７ー１３（比例４数はいれかえても比例）
  による。
• 　Ｃ：Ｅ＝Ｄ：Ｆ
  となっている。

そして
　Ａは平面数であり、
　Ｃ、Ｄはその辺である

• 　命題の設定による。

から、
　ＤはＣにかけて
　Ａをつくった。
　　　　　　[......(２)]

• 　前節、
  　定義７ー１７（平面数）
  による。
• 　Ｄ×Ｃ＝Ａ
  となっている。

同じ理由で
　ＥもＦにかけてＢをつくった。
　　　　　　[......(３)]

• 　Ｅ×Ｆ＝Ｂ
  となっている。

そこで
　ＤがＥにかけてＧをつくる
とせよ。
　　　　　　[......(ａ)]

• 　推論の設定である。
• 　Ｄ×Ｅ＝Ｇ
  となっている。

そうすれば
　Ｄは
　ＣにかけてＡをつくり、
　ＥにかけてＧをつくった

• 　（２）、 （ａ）
  による。
• 　Ｄ×Ｃ＝Ａ、Ｄ×Ｅ＝Ｇ
  となっている。

から、
　ＣがＥに対するように、
　ＡがＧに対する。
　　　　　　[......(４)]

• 　前節、
  　命題７ー１７（同数を各項にかけても比は同じ）
  による。
• 　Ｃ：Ｅ＝Ａ：Ｇ
  となっている。

ところが
　ＣがＥに対するように、
　ＤがＦに対する。

• 　（１）による。

それゆえ
　ＤがＦに対するように、
　ＡがＧに対する。
　　　　　　[......(５)]

• 　前節、前々節、
  　命題５ー１１（同一の比に同じ比）
  による。
• 　Ｄ：Ｆ＝Ａ：Ｇ
  となっている。

また
　ＥはＤにかけてＧをつくり、
　ＦにかけてＢをつくった

• 　（ａ）、
  　命題７ー１６（積の可換性）、
  　（３）による。
• 　Ｅ×Ｄ＝Ｇ、Ｅ×Ｆ＝Ｂ
  となっている。

から、
　ＤがＦに対するように、
　ＧがＢに対する。

• 　前節、
  　命題７ー１７（同数を各項にかけても比は同じ）
  による。
• 　Ｄ：Ｆ＝Ｇ：Ｂ
  となっている。

ところが
　ＤがＦに対するように、
　ＡがＧに対する
ことは証明された。

• 　（５）による。

ゆえに
　ＡがＧに対するように、
　ＧがＢに対する。
　　　　　　[......(６)]

• 　前節、前々節、
  　命題５ー１１（同一の比に同じ比）
  による。
• 　Ａ：Ｇ＝Ｇ：Ｂ
  となっている。

したがって
　Ａ、Ｇ、Ｂは順次に比例する。

よって
　Ａ、Ｂの間には
　１つの比例中項数がある。

次に
　ＡはＢに対し
　対応する辺が
　対応する辺に対する比、
　すなわち
　ＣがＥに
　または
　ＤがＦに対する比の
　２乗の比をもつ
と主張する。

　Ａ、Ｇ、Ｂは順次に比例し、
　ＡはＢに対し、
　Ｇに対する比の２乗の比をもつ。

• 　（６）による。
• 　Ａ：Ｂ＝（Ａ：Ｇ）^2
  となっている。

そして
　ＡがＧに対するように、
　ＣがＥに、
　ＤがＦに
　対する。

• 　（４）、（１）、
  　命題５ー１１（同一の比に同じ比）
  による。

したがって
　ＡはＢに対し、
　ＣがＥに
　または
　ＤがＦに対する比の
　２乗の比をもつ。

• 　前節、
  　命題８ー１１の補足 （同じ比の２(3)乗の比は同じ）
  による。

　これが証明すべきことであった。

• 命題８ー１８は
  　Ａ＝Ｃ×Ｄ、
  　Ｂ＝Ｅ×Ｆ、
  　Ｃ：Ｅ＝Ｄ：Ｆ
  ならば、
  　Ａ、Ｂの間に比例中項数が入り、
  　Ａ：Ｅ×Ｄ
  　＝Ｅ×Ｄ：Ｂ
  かつ
  　Ａ：Ｂ＝（Ｃ：Ｅ）^2
  のことである。
  
• 　証明の過程から、
  　次のことがわかる。
  　相似な平面数において、
  　対応しない辺の積が
  　比例中項
  となる。
  (以下、命題８ー１８の補足 （構成.相似な平面数の比例中項数）という。)
  
• 命題８ー１８の補足 （構成.相似な平面数の比例中項数）

  前提	作図	推論
  定義
  公準
  公理
  命題		8-18
  その他

• 命題８ー１８は推論用命題である。

  前提	作図	推論
  定義		7-17,7-22
  公準
  公理
  命題		5-11,7-16,7-17,8-11補
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭