ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー１６（積の可換性）
(商は小さい) もし
　２つの数を互いにかけあわせて、
　ある数をつくる
ならば、
　これらの２つの積は
　互いに等しい
であろう。

• 数は、 定義７ー２による。
• かけるは、 定義７ー１６による。
• 積は、 定義７ー１６の補足２による。
• 等しいは、 公理１ー７による。

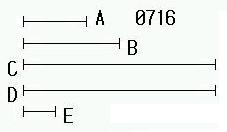
　Ａ、Ｂを２つの数
とし、

• 「数（について）・・・とせよ」は、
  コメント４（命題７ー１） 参照のこと。
• 　数Ａ、Ｂ
  をとっている。

　ＡはＢにかけてＣをつくり、
　ＢはＡにかけてＤをつくる
とせよ。

• 定義７ー１６（かける）
  により、
  Ｃは、
  ＢをＡ回くわえたものである。
  Ｄは、
  ＡをＢ回くわえたものである。
  
• 　Ａ×Ｂ＝Ｃ、
  　Ｂ×Ａ＝Ｄ
  となっている。

　ＣはＤに等しい
と主張する。

　ＡはＢにかけて
　Ｃをつくった
から、
　ＢがＣを割った商は
　Ａのなかにある単位の個数
である。

• 定義７ー１６（かける）、
  定義５ー１の補足４（割る）
  による。
• 　商(Ｃ,Ｂ)＝個数(Ａ,単位)＝ａ
  となっている。

ところが
　単位Ｅが数Ａを割った商も
　Ａのなかにある単位の個数である。

• 定義５ー１の補足４（割る）
  による。
• 　商(Ａ,単位Ｅ)＝個数(Ａ,単位)＝ａ
  となっている。

それゆえ
　単位Ｅが数Ａを、
　ＢがＣを
　割った商は等しい。

• 前節、前々節の結果、
  公理１ー１（同じものに等しい）
  による。
• 　商(Ａ,単位Ｅ)＝商(Ｃ,Ｂ)＝ａ
  となっている。

ゆえに
　いれかえて
　単位Ｅが数Ｂを、
　ＡがＣを
　割った商は等しい。
　　　　　　　　　　[......(ａ)]

• 命題７ー１５（割る数と商のいれかえ）
  による。
• 　商(Ｂ,単位Ｅ)＝商(Ｃ,Ａ)＝ｂ
  となっている。

また
　ＢはＡにかけて
　Ｄをつくった
から、
　ＡがＤを割った商は
　Ｂのなかにある単位の個数である。

• 定義７ー１６（かける）、
  定義５ー１の補足４（割る）
  による。
• 　商(Ｄ,Ａ)＝個数(Ｂ,単位)＝ｂ
  となっている。

したがって
　単位Ｅが数Ｂを、
　ＡがＤを
　割った商は等しい。

• 定義５ー１の補足４（割る）
  による。
• 　商(Ｂ,Ｅ)＝商(Ｄ,Ａ)＝ｂ
  となっている。

ところが
　単位Ｅが数Ｂを、
　ＡがＣを
　割った商は等しかった。

• （ａ）による。
• 　商(Ｂ,単位Ｅ)＝商(Ｃ,Ａ)＝ｂ
  となっている。

それゆえ
　ＡがＣ、Ｄの双方を割った商は等しい。

• 公理１ー１（同じものに等しい）による。
• 　商(Ｃ,Ａ)＝商(Ｄ,Ａ)＝ｂ
  となっている。

よって
　ＣはＤに等しい。

• 定義７ー８の補足（商）、
  公理１ー５の補足２（等しいもののｎ倍、ｎ倍に等しいもの）
  による。
• 　Ｃ＝Ｄ＝ｂＡ
  となっている。

これが証明すべきことであった。

• 　数Ａが数Ｐで割り切れる
  ならば、
  　商Ｑ(Ａ,Ｐ)
  をとれば、
  　命題７ー１５（割る数と商のいれかえ）
  により、
  　Ｐ;＝商(Ａ,Ｑ)
  となるので、
  　命題の補足（定義７ー３）（割り切る数は小さい）
  により
  　Ｑ＜Ａ
  となる。
  したがって、
  　数Ａが数Ｐで割り切れる
  ならば、
  　商Ｑ(Ａ,Ｐ)＜Ａ。 (以下、命題７ー１６の補足(商は小さい)という。)
  　
• 命題７ー１６は、
  　Ａ×Ｂ＝Ｃ、
  　Ｂ×Ａ＝Ｄ
  ならば、
  　Ｃ＝Ｄ
  つまり、
  　Ａ×Ｂ＝Ｂ×Ａ
  のことである。
  
  
• 命題７ー１６の補足(商は小さい)

  前提	作図	推論
  定義
  公準
  公理
  命題		補(義7-3),7-15
  その他

• 命題７ー１６は推論用命題である。

  前提	作図	推論
  定義		5-1補4,7-8補,7-16
  公準
  公理		1-5補2,1-1
  命題		7-15
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭