ユークリッド原論をどう読むか（１２）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第８巻
　
命題８ー１３（順次比例の２(3)乗も順次比例）
もし
　順次に比例する
　任意個の数があり、
　おのおのが２乗して
　ある数をつくる
ならば、
　それらからできた数は
　比例する
であろう。

そしてもし
　最初の数がこれらの数にかけて
　ある数をつくる
ならば、
　それらもまた比例する
であろう。

• 　後半は、
  　最初の数を３乗してできる数
  についてのべている。
  
• 順次に比例は、
  定義の補足（命題８ー１）による。
• 数は、
  定義７ー２による。
• ２乗は、
  定義７ー１９の補足による。
• 比例は、
  定義７ー２１による。
• かけるは、
  定義７ー１６による。

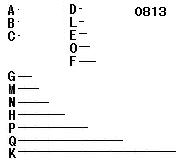
　順次に比例する任意個の数
　Ａ、Ｂ、Ｃがあり、

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
• 　準一般的な証明は、
  　コメント２（命題５ー１）
  　参照のこと。
• Ａ：Ｂ＝Ｂ：Ｃとなっている。

　ＡがＢに対するように、
　ＢがＣに対し、
　Ａ、Ｂ、Ｃが２乗して
　Ｄ、Ｅ、Ｆをつくり、
　Ｄ、Ｅ、Ｆにかけて
　Ｇ、Ｈ、Ｋをつくる
とせよ。
　　　　　　[......(ａ)]

• 　Ａ：Ｂ＝Ｂ：Ｃ、
  　Ａ×Ａ＝Ｄ、Ｂ×Ｂ＝Ｅ、
  　Ｃ×Ｃ＝Ｆ、
  　Ａ×Ｄ＝Ａ×Ａ×Ａ＝Ｇ、
  　Ｂ×Ｅ＝Ｂ×Ｂ×Ｂ＝Ｈ、
  　Ｃ×Ｆ＝Ｃ×Ｃ×Ｃ＝Ｋ
  　となっている。

　Ｄ、Ｅ、ＦとＧ、Ｈ、Ｋとは
　順次に比例する
と主張する。

　ＡはＢにかけてＬをつくり、
　Ａ、ＢはＬにかけて
　それぞれＭ、Ｎをつくる
とせよ。
　　　　　　[......(ｂ)]

• 　Ａ×Ｂ＝Ｌ、
  　Ａ×Ｌ＝Ａ×Ａ×Ｂ＝Ｍ、
  　Ｂ×Ｌ＝Ｂ×Ａ×Ｂ＝Ｎ
  　となっている。
  また、
  　命題７ー１６（積の可換性）
  により、
  　Ｂ×Ｌ＝Ｌ×Ｂ＝Ａ×Ｂ×Ｂ＝Ｎ
  　である。
  

そしてまた
　ＢはＣにかけてＯをつくり、
　Ｂ、ＣはＯにかけて
　それぞれＰ、Ｑをつくる
とせよ。
　　　　　　[......(ｃ)]

• 　Ｂ×Ｃ＝Ｏ、
  　Ｂ×Ｏ＝Ｂ×Ｂ×Ｃ＝Ｐ、
  　Ｃ×Ｏ＝Ｃ×Ｂ×Ｃ＝Ｑ
  　となっている。
  また、
  　命題７ー１６（積の可換性）
  により、
  　Ｃ×Ｏ＝Ｏ×Ｃ＝Ｂ×Ｃ×Ｃ＝Ｑ
  　である。
  

そうすれば
　前と同様にして
　Ｄ、Ｌ、ＥとＧ、Ｍ、Ｎ、Ｈとが
　Ａ対Ｂの比をなして
　順次に比例し、

• 　（ａ）、 （ｂ）
  により、
  　Ｄ＝Ａ×Ａ、Ｌ＝Ａ×Ｂ、Ｅ＝Ｂ×Ｂ、
  　Ｇ＝Ａ×Ａ×Ａ、Ｍ＝Ａ×Ａ×Ｂ、
  　Ｎ＝Ａ×Ｂ×Ｂ、Ｈ＝Ｂ×Ｂ×Ｂ
  　となっている
  ので、
  　命題７ー１７（同数を各項にかけても比は同じ）
  　命題７ー１８（各項を同数にかけても比は同じ）
  による。
  

また
　Ｅ、Ｏ、ＦとＨ、Ｐ、Ｑ、Ｋとが
　Ｂ対Ｃの比をなして
　順次に比例する
ことを証明しうる。

• 　（ａ）、 （Ｃ）
  により、
  　Ｅ＝Ｂ×Ｂ、Ｏ＝Ｂ×Ｃ、Ｆ＝Ｃ×Ｃ、
  　Ｈ＝Ｂ×Ｂ×Ｂ、Ｐ＝Ｂ×Ｂ×Ｃ、
  　Ｑ＝Ｂ×Ｃ×Ｃ、Ｋ＝Ｃ×Ｃ×Ｃ
  　となっている
  ので、
  　命題７ー１７（同数を各項にかけても比は同じ）
  　命題７ー１８（各項を同数にかけても比は同じ）
  による。
  

そして
　ＡがＢに対するように、
　ＢがＣに対する。

• 　（ａ）による。

それゆえ
　Ｄ、Ｌ、Ｅは
　Ｅ、Ｏ、Ｆと同じ比をなし、
また
　Ｇ、Ｍ、Ｎ、Ｈも
　Ｈ、Ｐ、Ｑ、Ｋと同じ比をなす。

• 　前節、前々節、
  　命題５ー１１（同一の比に同じ比）
  による。
  

そして
　Ｄ、Ｌ、Ｅは
　Ｅ、Ｏ、Ｆと
　同じ個数であり、
　Ｇ、Ｍ、Ｎ、Ｈは
　Ｈ、Ｐ、Ｑ、Ｋと
　同じ個数である。

ゆえに
　等間隔比により
　ＤがＥに対するように、
　ＥがＦに対し、
　ＧがＨに対するように、
　ＨがＫに対する。

• 　命題７ー１４（数の等間隔比）
  による。

　これが証明すべきことであった。

• 　Ａ：Ｂ＝Ｂ：Ｃ
  ならば
  　Ａ^2：Ｂ^2＝Ｂ^2：Ｃ^2、
  かつ
  　Ａ^3：Ｂ^3＝Ｂ^3：Ｃ^3
  のことである。
• 命題８ー１３は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理
  命題		5-11,7-14,7-16,7-17,7-18
  その他	コ4(題7-1)	コ2(題5-1)

前 　　 次 　　 目次 　　頁頭