ユークリッド原論をどう読むか(12)
頁末
前
次
目次
ユークリッド原論
第8巻
命題8ー9(互に素な数間の順次比例挿入項)
もし
二つの数が互いに素であり、
それらの間に
順次に比例する数が入る
ならば、
いくつの数が順次に比例して
それらの間に入ろう
と、
同じ個数の数が順次に比例して
もとの2数の双方と
単位との間にも入る
であろう。
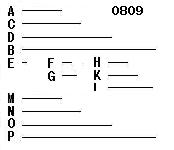
A、Bを
互いに素である2数
とし、
それらの間に順次に比例する
[入る限り入れる
として、]
C、Dが入る
とし、
-
準一般的な証明である。
コメント2(命題5ー1)参照のこと。
-
命題8ー8の補足(構成.順次比例項の挿入)
による。
-
例えば、
16と81の間に
順次に比例するように項をいれる
とすれば、
16、36、81と
16、24、36、54、81との
2つの入れ方がある。
本命題の趣旨からすると、
後者に限る
と見るのが
妥当である。
そして
単位Eが定められた
とせよ。
いくつの数が順次に比例して
A、Bの間に入ろう
と、
同じ個数の数が
順次に比例して
A、Bの双方と
単位との間にも入るであろう
と主張する。
A、C、D、Bの比をなす
最小である二つの数
F、Gが、
-
命題8ー2(構成.順次に比例する最小の数)
による。
-
A:C=C:D=D:B
=F:G
となっていて、
F、Gは、最小となっている。
三つの数H、K、Lがとられ、
-
命題8ー2(構成.順次に比例する最小の数)
による。
-
A:C=C:D=D:B
=H:K=K:L
となっていて、
H、K、Lは最小となっている。
そして
次々に一つずつ多くして、
A、C、D、Bと
同じ個数になるまで
せよ。
かかる数がとられた
とし、
それらをM、N、O、P
とせよ。
-
構成方法は前節と同じである。
A:C=C:D=D:B
=M:N=N:O=O:P
となっていて、
M、N、O、Pは最小となっている。
そうすれば
Fが2乗してHをつくり、
HにかけてMをつくり、
Gが2乗してLをつくり、
LにかけてOをつくった
ことは明らかである。
[......(a)]
-
命題8ー2(構成.順次に比例する最小の数)
による。
そして
M、N、O、Pは
F、Gと
同じ比をもつ数のうちで
最小であり、
A、C、D、Bも
F、Gと
同じ比をもつ数のうちで
最小であり、
M、N、O、Pは
A、C、D、Bと
同じ個数である
-
命題8ー2(構成.順次に比例する最小の数)
による。
から、
M、N、O、Pのおのおのは
A、C、D、Bのおのおのに等しい。
-
前者の各数と後者の各数は、
互いに他と等しいか大きい
ので、
公理1ー7の補足(線分・角は大か等か小)
により
それぞれ等しい。
それゆえ
MはAに、
OはBに等しい。
[......(1))]
そして
Fは2乗してHをつくった
から、
FがHを割った商は
Fのなかにある単位の個数である。
ところが
単位EがFを割った商も
Fのなかにある単位の個数である。
ゆえに
単位Eが数Fを、
FがHを割った商は等しい。
したがって
単位Eが数Fに対するように、
FがHに対する。
[......(2)]
また
FがHにかけてMをつくった
から、
HがMを割った商は
Fのなかにある単位の個数である。
ところが
単位Eが
数Fを≪も≫[割]った商も
Fのなかにある単位の個数である。
それゆえ
単位Eが数Fを、
HがMを割った商は等しい。
ゆえに
単位Eが数Fに対するように、
HがMに対する。
ところが
単位Eが数Fに対するように、
FがHに対する
ことが先に証明された。
したがって
単位Eが数Fに対するように、
FがHに、
HがMに対する。
しかも
MはAに等しい。
それゆえ
単位Eが数Fに対するように、
FがHに、
HがAに対する。
同じ理由で
単位Eが数Gに対するように、
GがLに、
LがBに対する。
ゆえに
いくつの数が順次に比例して
A、Bの間に入ろう
と、
同じ個数の数が順次に比例して
A、Bの双方と
単位Eの間にも入る
であろう。
これが証明すべきことであった。
-
すなわち、
AがBに素であり、
かつ
A:C=C:D=D:B
ならば、
同じ個数の数が
1とA、
および
1とBとの間に入る.
- 命題8ー9は推論用命題である。
前
次
目次
頁頭
