ユークリッド原論をどう読むか（９）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー２５（比例の最大最小項の和は大きい）
もし
　４つの量が比例するならば、
　最大と最小の和は
　残りの２つの和より大きい 。

• 量は、定義５ー１の補足 による。
• 比例は、定義５ー６ による。
• 最大・最小は、 定義の補足３（命題３ー７） による。
• 大きいは、公理１ー８ による。

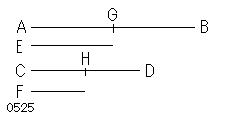
４つの量 ＡＢ、ＣＤ、Ｅ、Ｆが比例する、
　すなわち
　ＡＢがＣＤに対するように、
　ＥがＦに対するとし、

• 同じ比をもつ線分の作図（仮想的）は、
  　コメント２（命題５ー４）参照のこと。
• 　量ＡＢ、ＣＤ、Ｆ に対して、 　Ｅ[;;ＡＢ：ＣＤ＝Ｅ：Ｆ]
  をとっている。

　ＡＢがそれらの最大、
　Ｆが最小とせよ。

• 　ＡＢ＞ＣＤ,Ｅ
  となっている。
  このとき、
  　定義５ー５（同じ比）
  により、
  　Ｅ＞Ｆ、
  　命題５ー１４（同じ比の前(後)項の大等小）
  により
  　ＣＤ＞Ｆ
  となり、
  　ＡＢ＞ＣＤ,Ｅ＞Ｆ
  となる。
  すなわち、
  　Ｆは最小
  となっている。
  

ＡＢ、Ｆの和は
　ＣＤ、Ｅの和より大きい
　と主張する。

ＡＧをＥに、
　ＣＨをＦに等しくせよ。【・・・(a)】

• 推論の設定である。
• 命題１ー３の補足（作図.等しい線分となる点）
  による。
• 　Ｇ(ＡＢ;;ＡＧ＝Ｅ)、
  　Ｈ(ＣＤ;;ＣＨ＝Ｆ)
  をとっている。

ＡＢがＣＤに対するように、
　ＥがＦに対し、

• 命題の設定 による。
• 　ＡＢ：ＣＤ＝Ｅ：Ｆ
  となっている。

　ＥはＡＧに、
　ＦはＣＨに等しいから、

• (a) による。
• 　Ｅ＝ＡＧ、
  　Ｆ＝ＣＨ
  となっている。

　ＡＢがＣＤに対するように、
　ＡＧがＣＨに対する。

• 命題の設定 、命題５ー１１の補足２ （等しい量は同じ比をもつ）
  による。
• 　ＡＢ：ＣＤ＝ＡＧ：ＣＨ
  となっている。

そして
　ＡＢ全体がＣＤ全体に対するように、
　引き去られた部分ＡＧが
　　引き去られた部分ＣＨに対するから、

• 命題５ー１９ （引き去りが比例なら残りも比例）
  の表現に合せている。
• 　ＡＢ：ＣＤ＝ＡＧ：ＣＨ
  となっている。

　残りのＧＢも残りのＨＤに対し、
　ＡＢ全体がＣＤ全体に対するようであろう。【・・・(1)】

• 命題５ー１９ （引き去りが比例なら残りも比例）
  による。
• 　ＧＢ：ＨＤ＝ＡＢ：ＣＤ
  となっている。

ところが
　ＡＢはＣＤより大きい。

• 命題の設定 による。
• 　ＡＢ＞ＣＤ
  となっている。

それゆえ
　ＧＢもＨＤより大きい。【・・・(2)】

• (1) ,命題５ー１６の補足 （同じ比の項の大等小２）
  による。
• 　ＧＢ＞ＨＤ
  となっている。

そして
　ＡＧはＥに、
　ＣＨはＦに等しいから、

• (a) による。
• 　ＡＧ＝Ｅ、
  　ＣＨ＝Ｆ
  となっている。

　ＡＧ、Ｆの和は
　ＣＨ、Ｅの和に等しい。【・・・(3)】

• 公理１ー２ （等しいものに等しいものを加える）
  による。
• 　ＡＧ＋Ｆ＝ＣＨ＋Ｅ
  となっている。

そしてもし
　ＧＢ、ＨＤが等しくなく、
　ＧＢが大きく、

• (2) による。
  もしと表現されているが、
  　ここではＧＢが大きい。
• 　ＧＢ＞ＨＤ
  となっている。

　ＧＢにＡＧ、Ｆが加えられ、
　ＨＤにＣＨ、Ｅが加えられるならば、
　ＡＢ、Ｆの和は
　ＣＤ、Ｅの和より大きい。

• (3) ,公理１ー４ （不等なものに等しいものを加える）
  による。
• 　ＡＢ＋Ｆ
  　＝ＧＢ＋ＡＧ＋Ｆ
  　＞ＨＤ＋ＣＨ＋Ｅ
  　＝ＣＤ＋Ｅ
  となっている。

よってもし
　４つの量が比例するならば、
　最大と最小の和は
　残りの２つの和より大きい。
これが証明すべきことであった。

• 命題５ー２５は、
  　ＡＢ：ＣＤ＝Ｅ：Ｆ、
  　ＡＢが最大
  ならば、
  　ＡＢ＋Ｆ＞ＣＤ＋Ｅのことである。
  
• 命題５ー２５は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理		1-2,1-4
  命題		1-3補,5-11補2,5-16補,5-19
  その他		コ2(題5-4)

前 　　 次 　　 目次 　　頁頭