ユークリッド原論をどう読むか（９）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー２４（各量の同じ比の和は同じ比）
もし
　第１の量が第２に対し、
　第３が第４に対すると同じ比 をもち、
　第５が第２に対し、
　第６が第４に対すると同じ比 をもつならば、
　第１と第５の和は
　第２に対し、
　第３と第６の和が第４に対すると同じ比 を
　もつであろう。

• 量は、定義５ー１の補足 による。
• 対する・ようには 定義の補足３（命題５ー１１） による。
• 同じ比は、定義５ー５ による。

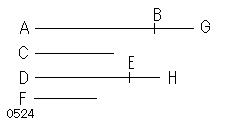
第１の量ＡＢが第２のＣに対し、
　第３のＤＥが第４のＦに対すると同じ比 をもち、
　第５のＢＧが第２のＣに対し、
　第６のＥＨが第４のＦに対すると同じ比 をもつ
　とせよ。

• 同じ比をもつ線分の作図（仮想的）は、
  　コメント２（命題５ー４）参照のこと。
• 　量ＡＢ、Ｃ、ＤＥ
  に対して、
  　Ｇ[延長ＡＢ]、
  　Ｆ[;;ＡＢ：Ｃ＝ＤＥ：Ｆ]、
  　Ｈ(延長ＤＥ;;ＢＧ：Ｃ＝ＥＨ：Ｆ)
  をとっている。

第１と第５の和ＡＧは
　第２のＣに対し、
　第３と第６の和ＤＨが第４のＦに対すると同じ比 をもつ
　であろうと主張する。

• 量の和は、
  命題の補足（定義５ー１４）（作図.量の和）
  による。

ＢＧがＣに対するように、
　ＥＨがＦに対するから、

• 命題の設定 による。
• 　ＢＧ：Ｃ＝ＥＨ：Ｆ
  となっている。

　逆に
　ＣがＢＧに対するように、
　ＦがＥＨに対する。【・・・(1)】

• 命題５ー１１の補足 （同じ比は互いに同じ）
  による。
• 　Ｃ：ＢＧ＝Ｆ：ＥＨ
  となっている。

そこで
　ＡＢがＣに対するように、
　ＤＥがＦに対し、
　ＣがＢＧに対するように、
　ＦがＥＨに対するから、

• 命題の設定 ,(1) による。
• 　ＡＢ：Ｃ＝ＤＥ：Ｆ、
  　Ｃ：ＢＧ＝Ｆ：ＥＨ
  となっている。

　等間隔比 により
　ＡＢがＢＧに対するように、
　ＤＥがＥＨに対する。【・・・(2)】

• 命題５ー２２ （等間隔比と同じ比）
  による。
• 　ＡＢ：ＢＧ＝ＤＥ：ＥＨ
  となっている。

そして
　量が分割比 により比例 するから、
　合比 によっても比例 するであろう。

• 命題５ー１８ （比例ならば合比も比例）
  である。

それゆえ
　ＡＧがＧＢに対するように、
　ＤＨがＨＥに対する。【・・・(3)】

• (2) ,命題５ー１８ （比例ならば合比も比例）
  による。
• 　ＡＧ：ＧＢ＝ＤＨ：ＨＥ
  となっている。

ところが
　ＢＧがＣに対するように、
　ＥＨがＦに対する。

• 命題の設定 による。
• 　ＢＧ：Ｃ＝ＥＨ：Ｆ
  となっている。

ゆえに
　等間隔比 により
　ＡＧがＣに対するように、
　ＤＨがＦに対する。

• (3) ,命題５ー２２ （等間隔比と同じ比）
  による。
• 　ＡＧ：Ｃ＝ＤＨ：Ｆ
  となっている。

よってもし
　第１の量が第２に対し、
　第３が第４に対すると同じ比 をもち、
　第５が第２に対し、
　第６が第４に対すると同じ比 をもつならば、
　第１と第５の和は
　第２に対し、
　第３と第６の和が第４に対すると同じ比 をもつ
　であろう。
これが証明すべきことであった。

• 命題５ー２４は、
  　Ａ：Ｃ＝Ｄ：Ｆ、
  　Ｂ：Ｃ＝Ｅ：Ｆ
  ならば、
  　（Ａ＋Ｂ）：Ｃ＝（Ｄ＋Ｅ）：Ｆ
  のことである。。
• 命題５ー２４は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理
  命題	補(義5-14)	5-11補 ,5-18 ,5-22
  その他		コ2(題5-4)

前 　　 次 　　 目次 　　頁頭