ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー２３（同じ線分の同じ側の相似な切片は唯一）

同じ線分の上に
　同じ側に
　円の相似で不等な
　２つの切片は
　つくられ得ない。

• 線分は、 定義の補足（命題１ー１） による。
• 同じ側は、 定義１ー７の補足 による。
• 円は、 定義１ー１５ による。
• 相似は、 定義３ー１１ による。
• 不等は、 定義の補足（公理１ー４） による。
• 切片は、 定義３ー６ による。

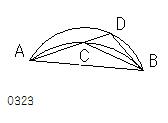
もし可能ならば、

• 背理法の仮定を述べようとしている。
• 「もし可能ならば」は、
  コメント２(命題１−７）参照のこと。

　同じ線分ＡＢ上に
　同じ側に
　円の相似で不等な
　２つの切片ＡＣＢ、ＡＤＢが
　つくられたとし、

• 背理法の仮定を述べている。
• 　線分ＡＢ
  に対して、
  　切片ＡＣＢ[ＡＢ]、
  　切片ＡＤＢ[ＡＢ;;同側(ＡＢ,弧ＡＣＢ),切片ＡＤＢ∽切片ＡＣＢ]、
  をとっている。
• 相似な切片は、
  　 定義３ー１１ （相似な切片）
  により、
  　「切片の角が等しい、
  　すなわち
  　切片内の角が等しい。」である。
  したがって
  　同じ線分上で
  　同じ側で
  　　相似で不等な切片とは、
  　弦が等しく
  　切片内の角が等しいが
  　　重なり合わない
  　ものである。
  重なり合わない２円は、
  　交わっている場合と、
  　一方が他方の中にある場合
  　がある。
  交わっている場合、
  　２円の交点が
  　少なくとも３つある。
  ところが、
  　 命題３−５の補足 (２円の交点は２つ)
  により
  ２つの円周の交点は２点であり、
  　これは不可能である。
  あり得ない場合に対しては、
  　命題は成立しているとみなす。
  交わっていない場合
  すなわち、
  一方の切片の孤は
  　両端以外は
  　他方の切片の内側にあり、
  他方のの切片の孤は
  　両端以外は
  　前者の切片の外側にある場合は、
  　以下の通り。
• 　内.弧ＡＣＢ;内.切片ＡＤＢ
  となっている。

　ＡＣＤがひかれ、

• 内側にある前者の切片をＡＢＣとし、
  　外側にある後者の切片をＡＤＢとする。
  ＡＢＣの孤の両端以外のところに
  　 公準１ー１の補足 （作図.任意の点をとる）
  により
  　点Ｃをとり、
  　溯ってＣを用いている。
  公準１ー１ （作図.直線）
  により
  　ＡとＣを結ぶ。
  公準１ー２ （作図.直線の延長）
  により
  　ＡＣをＣの方向に延長すると、
  　Ｃは切片ＡＤＢの内部の点であるから
  命題３−２の補足 (円内通過直線は円周と２交点)
  により
  　Ａ以外に
  　切片ＡＤＢの孤と１点Ｄで交わる。
  　このＤを溯って用いている。
• 　点Ｃ[弧ＡＣＢ]、
  　交点Ｄ(延長ＡＣ,弧ＡＤＢ)
  をとっている。

　ＣＢ、ＤＢが結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 　線分ＣＢ、ＤＢ
  をとっている。

そうすれば

切片ＡＣＢは
　切片ＡＤＢに
　相似であり、
円の相似な切片は
　等しい角を含むものであるから、

• すなわち、
  　切片内の角が等しいものであるから、
  
• 　切片ＡＣＢ∽切片ＡＤＢ
  となっている。

角ＡＣＢは
　角ＡＤＢに等しい、

• 定義３ー１１ （相似な切片）
  による。
• 　∠ＡＣＢ＝∠ＡＤＢ
  となっている。

　すなわち
　外角が内角に等しい。
これは不可能である。

• 命題１ー１６ （外角と内対角）
  による。
• 　∠ＡＣＢ＞∠ＡＤＢ
  となるべきであった。

したがって、
［２つの場合の結果により、
　切片ＡＤＢとＡＣＢは一致する。］

• 背理法による。
  
• 　切片ＡＤＢ≡切片ＡＣＢ
  となっている。

よって
　同じ線分の上に
　同じ側に
　円の相似で不等な
　２つの切片はつくられ得ない。
これが証明すべきことであった。

• 命題３ー２３は、
  　線分ＡＢ
  に対して、
  　切片ＡＣＢ[ＡＢ]、
  　切片ＡＤＢ[ＡＢ;;同側(ＡＢ,弧ＡＣＢ),切片ＡＤＢ∽切片ＡＣＢ]、
  をとれば、
  　切片ＡＣＢ≡切片ＡＤＢ
  のことである。
  
• 命題３ー２３は推論用命題である。

  前提	作図	推論
  定義		3-11 ,補(題3-16)
  公準	1-1,1-1補 ,1-2
  公理
  命題	3-2補,3-5補	1-16 ,3-6補5,3-6補6
  その他		背理法,コ2(題1-7)、場合分け

前 　　 次 　　 目次 　　頁頭