ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー２４（等しい線分の相似な切片は等しい）

　等しい線分上にある、
　円の相似な切片は
　互いに等しい。

• 等しいは、 公理１ー７ による。
• 線分は、 定義の補足（命題１ー１） による。
• 円は、 定義１ー１５ による。
• 相似な切片は、 定義３ー１１ による。

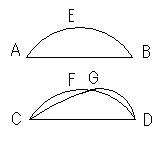
ＡＥＢ、ＣＦＤを
　等しい線分ＡＢ、ＣＤ上にある、
　円の相似な切片とせよ。

• 　線分ＡＢ
  に対して、
  　線分ＣＤ[;;ＣＤ＝ＡＢ]、
  　切片ＡＥＢ[ＡＢ]、
  　切片ＣＦＤ(ＣＤ;;切片ＣＦＤ∽ＡＥＢ)
  をとっている。

切片ＡＥＢは
　切片ＣＦＤに等しい
　と主張する。
切片ＡＥＢが
　切片ＣＦＤの上に重ねられ、

• 必要があれば、
  　回転して、
  　弦の同じ側に
  　孤がくるようにする。

　点ＡがＣの上に、
　線分ＡＢがＣＤの上におかれるとき、
ＡＢは
　ＣＤに等しいから、
点Ｂも
　点Ｄの上に重なるであろう。

• 公理１−７ （等しい）
  による。
• 　線分ＡＢ≡線分ＣＤ
  となっている。

また
　ＡＢが
　ＣＤの上に重なるとき、
切片ＡＥＢも
　ＣＦＤに重なるであろう。

• 弦が重ね合わされたから、
  　同一線分上に相似な切片を作るという
  　 命題３ー２３ （同じ線分の同じ側の相似な切片は唯一）
  の設定と一致し、
  　ただちに、結論がしたがう。
  
• 　切片ＡＥＢ≡切片ＣＦＤ
  となっている。

≪なぜならもし
　線分ＡＢが
　ＣＤの上に重なるが、
切片ＡＥＢは
　ＣＦＤの上に重ならないならば、
　ＣＦＤの内部におちるか
　外部におちるか
　または
　ＣＧＤのようにずれるであろう。
そして
　円が円と
　２つより多くの点で
　交わることになる。
これは不可能である。
≫

• 「なぜならもし」については、
  　コメント（命題１ー４）を参照のこと。
• 上記の文は、
  　背理法によらなくても
  　 命題３ー２３ （同じ線分の同じ側の相似な切片は唯一）
  により、
  　証明が成立するので
  　必要ない。
  場合分けをしているが、
  　その後の論証においては、
  　その１つの場合のみに
  　対応しているにすぎない。
  

それゆえ
　ＡＢがＣＤの上に重ねられるとき、
　切片ＡＥＢも
　ＣＦＤの上に重ならないことはないであろう。
ゆえに
　かさなり、それに等しいであろう。
よって、
　等しい線分上にある、
　　円の相似な切片は
　互いに等しい。

• 命題１ー４ （２辺挟角相等）
  の後、
  　再度
  　明確に現れた
  　重ね合わせの論法である。
• 命題３ー２４は、
  　線分ＡＢ
  に対して、
  　線分ＣＤ[;;ＣＤ＝ＡＢ]、
  　切片ＡＥＢ[ＡＢ]、
  　切片ＣＦＤ(ＣＤ;;切片ＣＦＤ∽ＡＥＢ)
  をとれば、
  　切片ＡＥＢ≡切片ＣＦＤ
  のことである。
  
• 命題３ー２４は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理		1-7
  命題		3-23
  その他		コ(題1-4)fi

前 　　 次 　　 目次 　　頁頭