ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー２２（内接四辺形の対角の和は２直角）　
内接

円に内接する
　四辺形の対角の和は
　２直角に等しい。

• 円は、 定義１ー１５ による。
• 内接は、
  　 定義３ー３ に準じて、
  　円の内部にあって、
  　円に会し、
  　円と交わらないことである。
  　（以後、定義の補足（命題３ー２２）(内接)という。）
• 四辺形は、 定義１ー１９ による。
• 対角は、 定義１ー２２の補足 による。
• 直角は、 定義１ー１０ による。
• 等しいは、 公理１ー７ による。

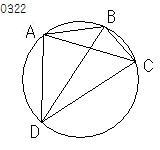
ＡＢＣＤを円とし、
　ＡＢＣＤを
　それに内接する四辺形とせよ。

• 　円ＡＢＣＤ
  に対して、
  　四辺形ＡＢＣＤ;（内接）円ＡＢＣＤ
  をとっている。

対角の和は
　２直角に等しい
　と主張する。

ＡＣ、ＢＤが結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 線分ＡＣ、ＢＤ
  をとっている。

そうすれば
　すべての三角形において
３つの角の和は
　２直角に等しいから、

• 命題１ー３２ （三角形の内対角・内角の和）
  である。

　三角形ＡＢＣの
３つの角
　ＣＡＢ、ＡＢＣ、ＢＣＡの和は
　２直角に等しい。

• 　∠ＣＡＢ＋∠ＡＢＣ＋∠ＢＣＡ＝２∠Ｒ
  となっている。

ところが
角ＣＡＢは
　角ＢＤＣに等しい、
　なぜなら
　同じ切片ＢＡＤＣ内にあるから。

• 命題３ー２１ （切片内の角は等しい）
  による。
• 　∠ＣＡＢ＝∠ＢＤＣ
  となっている。
• 「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６）を参照のこと。

そして
角ＡＣＢは
　角ＡＤＢに等しい、
　なぜなら
　同じ切片ＡＤＣＢ内にあるから。

• 命題３ー２１ （切片内の角は等しい）
  による。
• 　∠ＡＣＢ＝∠ＡＤＢ
  となっている。
• 「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６）を参照のこと。

それゆえ
角ＡＤＣ全体は
　角ＢＡＣ、ＡＣＢの和に等しい。

• 公理１ー７ （等しい） による。
• 　∠ＡＤＣ＝∠ＢＡＣ＋∠ＡＣＢ
  となっている。

双方に
　角ＡＢＣが加えられたとせよ。
そうすれば
角ＡＢＣ、ＢＡＣ、ＡＣＢの和は
　角ＡＢＣ、ＡＤＣの和に等しい。

• 公理１ー２ （等しいものに等しいものを加える）
  による。
• 　∠ＡＢＣ＋∠ＢＡＣ＋∠ＡＣＢ
  　＝∠ＡＢＣ＋∠ＡＤＣ
  となっている。 　

ところが
角ＡＢＣ、ＢＡＣ、ＡＣＢの和は
　２直角に等しい。

• 命題１ー３２ （三角形の内対角・内角の和）
  による。
• 　∠ＡＢＣ＋∠ＢＡＣ＋∠ＡＣＢ
  　＝２∠Ｒ
  となっている。

したがって
　角ＡＢＣ、ＡＤＣの和も
　２直角に等しい。

• 公理１ー１ （同じものに等しい）
  による。
• 　∠ＡＢＣ＋∠ＡＤＣ
  　＝２∠Ｒ
  となっている。

同様にして
　角ＢＡＤ、ＤＣＢの和が
　２直角に等しいことも証明し得る。

• 角ＢＡＤ、ＤＣＢも
  　円に内接する四辺形の
  　　対角であるから、
  　言及している。
• 　∠ＢＡＤ＋∠ＤＣＢ＝２∠Ｒ

よって、
円に内接する
　四辺形の対角の和は
　２直角に等しい。
これが証明すべきことであった。

• 命題３ー２２は、
  　円ＡＢＣＤ
  に対して、
  　四辺形ＡＢＣＤ;（内接）円ＡＢＣＤ
  をとれば、
  　∠ＡＢＣ＋∠ＡＤＣ＝２∠Ｒ、
  　∠ＢＡＤ＋∠ＤＣＢ＝２∠Ｒ
  のことである。
  
• 命題３ー２２は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理		1-1 ,1-2 ,1-7
  命題		1-32 ,3-21
  その他		コ2(題1-16)f

前 　　 次 　　 目次 　　頁頭