ユークリッド原論をどう読むか（６）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー１０（２円の交点は２点まで）　
（３点共有で円が一致）
円は
　円と
　二つより多くの点で
　交わらない。

• この命題においては、
  　他の命題のような
  　図による題意の説明がない。
  原論において
  　初めてのスタイルである。
• 円は、定義１ー１５ による。
• 点は、定義１ー１ による。
• 交わるは、定義１−８の補足 による。

もし可能ならば、

• 以下が
  　背理法の仮定であることを示している。
• 「もし可能ならば」は、
  コメント２(命題１−７）参照のこと。

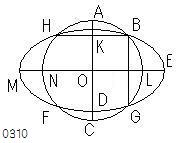
円ＡＢＣが
　円ＤＥＦと
　二つより多くの
　 点Ｂ、Ｇ、［Ｆ、］Ｈで交わるとし、

• 以上が帰納法の仮定である。
  ３点で済ませられないかが
  　課題として残る。
  しかし、
  　以下の証明では、
  　交点は
  　３点の存在しか前提としていないので、
  　論証は成立している。

ＢＨ、ＢＧが結ばれ、

• 公準１ー１ による。

点Ｋ、Lで
　［それぞれ］２等分されたとせよ。 【・・・(a)】

• 命題１ー１０ による。

そして
　Ｋ、Lから
I,J 　［それぞれ］ＢＨ、ＢＧに直角に
　ＫＣ、ＬＭがひかれ、
　点Ａ、Ｅまで延長されたとせよ。

• 命題１ー１１ による。
• 命題３ー２の補足 により、
  　Ｋを通る直線は、
  　それぞれの円周と２点で交わる。
  一方の円周との交点をＡ、Ｃとし、
  　他方の円周との交点の一つをＤとする。
  Ｌを通る直線も
  　それぞれの円周と２点で交わる。
  前者の円周との交点をＬ、Ｎとし、
  　後者の円周との交点をＭ、Ｅとする。
  これらの点のうち、
  　Ａ、Ｃ、Ｅ、Ｄについて溯って用いている。

そうすれば、
　円ＡＢＣにおいて
　弦ＡＣが
　弦ＢＨを直角に２等分するから、
円ＡＢＣの中心はＡＣ上にある。 【・・・(1)】

• (a) ,命題３ー１の系 による。

また
　同じ円ＡＢＣにおいて
　弦ＬＮが
　弦ＢＧを直角に２等分するから、 円ＡＢＣの中心は
　ＬＮ上にある。

• (a) ,命題３ー１の系 による。

ところが
　ＡＣ上にあることも
　先に［(1)で］ 証明され、
しかも
　弦ＡＣ、ＬＮは
　Ｏ以外のいかなる点でも交わらない。

• 命題１ー３１の補足２ により、
  　ＡＣ、ＬＮは交わり、
  　その交点をＯとする。
  公理１ー９ により、
  　交点はＯしかない。

それゆえ
　点Ｏは
　円ＡＢＣの中心である。

• 命題３ー１ により
  　中心はただ一つ存在し、
  　それがＡＣ上で、
  　かつ
  　ＬＮ上であるから、
  　Ｏ以外でありえない。
  つまり、中心はＯである。

同様にして
　Ｏは
　また
　円ＤＥＦの中心である
　ことも証明しうる。

• 線分ＢＧ、ＢＨは
  　円ＤＥＦの弦でもあるから。

ゆえに
　互いに交わる二つの円ＡＢＣ、ＤＥＦが
　同じ中心Ｏをもつ。
これは不可能である。

• 命題３ー５ により、
  　交わる２円は
  　異なる中心をもつから。
• 背理法により
  　証明が成立したことになる。

よって
　円は
　円と二つより多くの点で交わらない。
これが証明すべきことであった。

• ２つの円が３点を共有すれば一致する。
  （以下、命題３ー１０の補足（３点共有で円が一致）という。）
  背理法の仮定として、
  もし、
  　異なる２円になる
  とすれば、
  　命題３−５の補足
  により、
  　共有点は２点となり、
  　矛盾する
  ので、
  背理法により結論を得る。
  
• 命題３ー１０の補足（３点共有で円が一致）

  前提	作図	推論
  定義
  公準
  公理
  命題		3-5補
  その他		背理法

• 命題3-10は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理		1-9
  命題	1-10 ,1-11 ,1-31補2 ,3-1	3-1系 ,3-5
  その他		背理法,コ2(題1-7)

前 　　 次 　　 目次 　　頁頭