ユークリッド原論をどう読むか（６）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー１１（内接２円の中心と接点）
もし
　二つの円が
　［一方が他方の］内側で互いに接し、
　それらの中心が
　とられるならば、
　それらの中心を結ぶ
　　線分は
　延長されて
　円の接点に落ちるであろう。

• 円は、定義１ー１５ による。
• 内側は、命題の補足３（定義１ー１４）による。
• 接するは、定義３−３による。
  内側でとは、
  　一方の内側において、
  　という意味である。
• 中心は、定義１ー１６ による。
• 線分は、定義の補足（命題１ー１） による。
• 接点は、定義３ー２の補足３による。

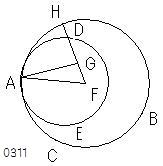
２円ＡＢＣ、ＡＤＥが
　［ＡＤＥがＡＢＣの］内側で
　点Ａにおいて接するとし、
　円ＡＢＣの中心Ｆと
　円ＡＤＥの中心Ｇと
　がとられたとせよ。 【・・・(a)】

• 命題３ー１（作図.円の中心） による。
• 　円ＡＢＣ
  に対して、
  　円ＡＤＥ[;;Ａ以外.円ＡＤＥ;内.円ＡＢＣ]
  　接点Ａ(円ＡＤＥ,円ＡＢＣ)、
  　中心Ｆ.円ＡＢＣ、
  　中心Ｇ.円ＡＤＥ
  をとっている。

Ｇ、Ｆを結ぶ線分は
　［ＦからＧに向かう方向に］延長されて

• 公準１ー１（作図.直線） 、公準１ー２（作図.直線の延長） による。

Ａに落ちるであろう
　と主張する。

• 命題３−２の補足(円内通過直線は円周と２交点) により、
  　２円の内部を通る半直線ＦＧは
  　２円の周と交わる。
  その交点が
  　接点であるということである。

そうでないとすれば、

• 背理法の仮定が
  　以下に続くことを示す。

もし可能ならば、

• 「もし可能ならば」は、
  コメント２(命題１−７）参照のこと。

ＦＧＨのようになるとし、

• 公準１ー２ (円内通過直線は円周と２交点) により、
  　線分ＦＧをＧの方向に延長して、
  　命題３−２の補足(円内通過直線は円周と２交点) により、
  　Ａと異なる
  　　点Ｄで
  　内側の円ＡＥＤと交わり
  　外に出て、
  　点Ｈで
  　外側の円ＡＣＢと交わるとし、
  　この点Ｄを溯って用いている。
• 　交点Ｄ(半直線ＦＧ,円ＡＤＥ);外.Ａ、
  　交点Ｈ(半直線ＦＧ,円ＡＣＢ);外.Ａ
  をとったとしている。

ＡＦ、ＡＧが
　結ばれたとせよ。

• 公準１ー１（作図.直線） による。
• 　線分ＡＦ、ＡＧ
  をとっている。

そうすれば、
　ＡＧ、ＧＦの和は
　ＦＡ、すなわちＦＨより大きいから、

• 命題１ー２０（三角形の２辺の和と１辺） 、
  　定義１ー１５（円） 、
  　公理１ー８の補足２（等より大・小、大・小に等） による。
• 　ＡＧ＋ＧＦ＞ＦＨ
  となっている。

双方から
　ＦＧが引き去られたとせよ。
そうすれば
　残りのＡＧは
　残りのＧＨより大きい。 【・・・(1)】

• 公理１ー４の補足２（不等なものから等しいものをひく） による。
• 　ＡＧ＞ＧＨ
  となっている。

ところが
　ＡＧはＧＤに等しい。

• (a) ,定義１ー１５（円） による。
• 　ＡＧ＝ＧＤ
  となっている。

ゆえに
　ＧＤはＧＨより大きい、

• 公理１ー８の補足２（等より大・小、大・小に等） による。
• 　ＧＤ＞ＧＨ
  となっている。

すなわち
　小さいものが
　大きいものより大きい。

• (1) 公理１ー８の補足（小さい） による。

これは不可能である。

• 背理法の仮定により
  　矛盾が生じた。

したがって
　Ｆ、Ｈを結ぶ線分は
　［円ＡＥＤの］外部に
　おちない［外部に出ない］
　であろう。

• 背理法による。
• 　線分ＦＨ;¬外.円ＡＥＤ
  となっている。

ゆえに
　Ａにおいて接点におちるであろう。 よってもし
　二つの円が
　内側で互いに接し、
　それらの中心が
　とられるならば、
　それらの中心を結ぶ線分は
　延長されて
　円の接点に落ちるであろう。
　
これが証明すべきことであった。

• 命題３ー６の補足(接する２円の接点と中心は１直線上) で述べた内容の一部である。
• 命題３ー１１は、
  　円ＡＢＣ
  に対して、
  　円ＡＤＥ[;;Ａ以外.円ＡＤＥ;内.円ＡＢＣ]
  　接点Ａ(円ＡＤＥ,円ＡＢＣ)
  であれば、
  　中心Ｆ.円ＡＢＣ、
  　中心Ｇ.円ＡＤＥ
  　点Ａ;上.直線(ＦＧ)
  のことである。
  
• 命題３ー１１は推論用命題である。

  前提	作図	推論
  定義		1-15
  公準	1-1 ,1-2
  公理		1-4補2 ,1-8補,1-8補2
  命題	3-1,3-2補	1-20
  その他		背理法,コ2(題1-7)

前 　　 次 　　 目次 　　頁頭