ユークリッド原論をどう読むか(4)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1−42(作図.角,三角形と平行四辺形)
与えられた直線角の中に
与えられた三角形に等しい
平行四辺形をつくること。
与えられた三角形をABC、
与えられた直線角をDとせよ。
このとき
直線角Dの中に
三角形ABCに等しい
平行四辺形をつくらねばならぬ。
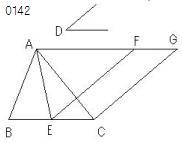
BCがEにおいて2等分され、
【・・・(a)】
- 命題1−10(作図・線分の2等分)
による。
-
中点E(BC)
をとっている。
AEが結ばれ、
- 公準1−1(作図.直線)
による。
-
線分AE
をとっている。
線分EC上に
その上の点Eにおいて
角Dに等しい角CEFがつくられ、
【・・・(b)】
- 命題1−23(作図・直線上に指定された角)
による。
- この論証では、
三角形の底辺の方に
角を移動しているが、
三角形を角の方に
移動することもできる。
命題1−10により
BCの中点Eをとり、
命題1−3により
ECに等しくなるように
角Dの辺上にDC’となるC’をとり、
公準1−1により
線分DC’をDの方に延長し、
再度命題1−3により
EBに等しくなるように
延長した直線上にDB’となるB’をとる。
直線B’C’について、
角Dの他方の辺と同じ側に、
命題1−7の補足により、
BA、CAにB’A’、C’A’が
それぞれ等しくなるように
点A’をとると、
三角形ABCとA’B’C’は等しい。
これで、角の方に三角形を移動できた。
-
半直線EF'[∠CEF'=∠D,同側(CE,A)]
をとっている。
Aを通り
ECに平行にAGがひかれ、
【・・・(c)】
- 命題1−31(作図・平行線)
による。
-
平行線AG'(A,EC)
をとっている。
Cを通り
EFに平行にCGがひかれたとせよ。
【・・・(d)】
- 与えられた角がCEFとなるので
BCとEFは交わり、
BCとAGは平行であるから
命題1−30の補足(交線に平行な線)
により
AGとEFは交わる。
この交点を改めてFとしている。
さらに
AGとEFが交わり
CGを
EFと平行になるように
ひいたのであるから
命題1−30の補足(交線に平行な線)
により
CGとAGは交わる。
この交点を改めてGとし、
CGと書いている。
-
交点F(EF',AG')、
交点G(AG',平行線(C,EF))
をとっている。
そうすれば
FECGは平行四辺形である。
【・・・(1)】
そして
BEはECに等しいから、
三角形ABEも三角形AECに等しい。
なぜなら
等しい底辺BE、ECの上にあり
かつ
同じ平行線BC、AGの間にある
から。
それゆえ
三角形ABCは
三角形AECの2倍である。
-
前節による。
-
△ABC=2×△AEC
となっている。
ところが
平行四辺形FECGも
三角形AECの2倍である。
なぜなら
それと同じ底辺をもち
かつ
それと同じ平行線の間にある
から。
- (1)
,
命題1−41(同一底辺上の平行四辺形と三角形の面積)
による。
-
平四FECG=2×△AEC
となっている。
ゆえに
平行四辺形FECGは
三角形ABCに等しい。
- 公理1−5(同じものの2倍)
による。
-
平四FECG=△ABC
となっている。
そして
与えられた角Dに
等しい角CEFをもつ。
よって
与えられた直線角の中に
与えられた三角形に等しい
平行四辺形をつくられた。
これが作図すべきものであった。
- この命題が、
直線図形を
指定された角におさまる
平行四辺形に
等積変形する第一歩である。
- 命題1-42は、
△ABC、
直線角D
に対して、
中点E(BC)、
半直線EF'(同側(CE,A);;∠CEF'=∠D,)、
平行線AG'(A,EC)、
交点F(EF',AG')、
交点G(AG',平行線(C,EF))、
をとれば、
平四FECG=△ABC
のことである。
- 命題1-42は作図用命題である。
前
次
目次
頁頭
