ユークリッド原論をどう読むか(4)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1ー38(三角形の等積変形2)
等しい底辺の上にあり
かつ
同じ平行線の間にある
三角形は
互いに等しい。
ABC、DEFを
等しい底辺BC、EFの上にあり
かつ
同じ平行線BF、ADの間にある
三角形とせよ。
-
線分BF
に対して、
点C[BF]、
点E(BF;;EF=BC)、
点A[外.BF]、
平行線AD(A,BC)、
△ABC、
△DEF
をとっている。
三角形ABCは
三角形DEFに等しいと主張する。
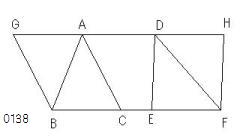
ADが
両方向にG、Hまで延長され、
- 公準1ー1(作図.直線)
による。
-
点G'[延長DA]、
点H'[延長AD]
をとっている。
Bを通りCAに平行に
BGがひかれ、
- 命題1ー31(作図・平行線)
により平行線がひかれ、
命題1ー30の補足(交線に平行な線)
により
この平行線とADの延長が交わる。
この交点を溯ってGとしている。
-
交点G(AD,平行線(B,CA))、
をとっている。
Fを通りDEに平行に
FHがひかれたとせよ。
【・・・(a)】
- 命題1ー31(作図・平行線)
により平行線がひかれ、
命題1ー30の補足(交線に平行な線)
により
この平行線とADの延長が交わる。
この交点を溯ってHとしている。
-
交点H(DA,平行線(F,ED))、
をとっている。
そうすれば
GBCA、DEFHの双方は
平行四辺形である。
そして
GBCAはDEFHに等しい。
【・・・(1)】
なぜなら
等しい底辺BC、EFの上にあり
かつ
同じ平行線BF、GHの間にあるから。
そして
三角形ABCは
平行四辺形GBCAの半分である。
【・・・(2)】
なぜなら
対角線ABがそれを2等分するから。
また
三角形FEDは
平行四辺形DEFHの半分である。
【・・・(3)】
なぜなら
対角線DFがそれを2等分するから。
ゆえに
三角形ABCは
三角形DEFに等しい。
よって
等しい底辺の上にあり
かつ
同じ平行線の間にある
三角形は互いに等しい。
これが証明すべきことであった。
- 直線図形は対角線を引くことにより、
三角形に分解される。
命題1ー34(平行四辺形の対辺・対角・対角線)
では、
平行四辺形が
対角線で2つの面積の等しい三角形に
分解される。
命題1ー38
により、
三角形の面積が
等積変形できることから、
任意の平面図形が
等積変形できる
道が開かれる。
- 本命題でも、
三角形の一部が重なる場合もあり得るが、
命題1ー36(平行四辺形の等積変形2)
のコメントに示したように、
双方の三角形と重ならない位置に
もう1つの三角形を想定することにより、
本命題で扱っている場合に帰着できる。
- 命題1-38は、
線分BF
に対して、
点C[BF]、
点E(BF;;EF=BC)、
点A[外.BF]、
平行線AD(A,BC)、
△ABC、
△DEF
をとれば、
△ABC=△DEF
のことである。
- 命題1-38は推論用命題である。
前
次
目次
頁頭
