ユークリッド原論をどう読むか（４）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１−４１（同一底辺上の平行四辺形と三角形の面積）
もし
　平行四辺形が
　三角形と同じ底辺をもち
　かつ
　同じ平行線の間にあれば、
　平行四辺形は
　三角形の２倍である。

• 平行四辺形は、定義の補足（命題１−３４）による。
• 三角形は、定義１−１９の補足２による。
• 底辺は、定義の補足（命題１−３５）、定義１−２０の補足２による。
• 平行線は、定義１−２３による。
• 倍は、定義の補足（公理１−５）による。

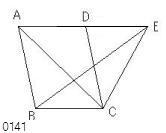
平行四辺形ＡＢＣＤが
　三角形ＥＢＣと同じ底辺をもち
　かつ
　同じ平行線ＢＣ、ＡＥの間にあるとせよ。

• 　平行四辺形ＡＢＣＤ
  に対して、
  　点Ｅ[直線ＡＤ]、
  　△ＥＢＣ
  をとっている。

平行四辺形ＡＢＣＤは
　三角形ＢＥＣの２倍である
　と主張する。
　


ＡＣが結ばれたとせよ。

• 公準１−１（作図.直線）
  による。
• 　線分ＡＣ
  をとっている。

そうすれば
　三角形ＡＢＣは三角形ＥＢＣに等しい。
　　　　　　【・・・(1)】
なぜなら
　それと同じ底辺ＢＣの上にあり
　かつ
　同じ平行線ＢＣ、ＡＥの間にあるから。

• 命題の設定 ,命題１−３９（三角形の等積変形の逆１）
  による。
• 「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６）を参照のこと。
• 　△ＡＢＣ＝△ＥＢＣ
  をとっている。

ところが
　平行四辺形ＡＢＣＤは
　三角形ＡＢＣの２倍である。
なぜなら対角線ＡＣが
　それを２等分するから。

• 命題１−３４（平行四辺形の対辺・対角・対角線）
  による。
• 「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６）を参照のこと。
• 　平四ＡＢＣＤ＝２×△ＡＢＣ
  となっている。

それゆえ
　平行四辺形ＡＢＣＤは
　三角形ＥＢＣの２倍でもある。

• (1) ,公理１−５（同じものの２倍）
  による。
• 　平四ＡＢＣＤ＝２×△ＥＢＣ
  となっている。

よってもし
　平行四辺形が
　三角形と同じ底辺をもち
　かつ
　同じ平行線の間にあれば、
　平行四辺形は三角形の２倍である。
　
これが証明すべきことであった。

• 命題1-41は、
  　平四ＡＢＣＤ
  に対して、
  　点Ｅ[直線ＡＤ]、
  　△ＥＢＣ
  をとれば、
  　平四ＡＢＣＤ＝△ＥＢＣ
  のことである。
  
• 命題1-41は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理		1-5
  命題		1-34、 1-39
  その他		コ2(題1-16)f

前 　　 次 　　 目次 　　頁頭