ユークリッド原論をどう読むか（４）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー３５（平行四辺形の等積変形１）　
底辺　

同じ底辺の上にあり
　かつ
　同じ平行線の間にある
　平行四辺形は
　互いに等しい。

• 平行四辺形（面積）における底辺は、
  　基底となっている動かさない辺をいう。
  　（以後、定義の補足（命題１ー３５）(底辺)という。）
• 平行線は、定義１ー２３による。
• 平行四辺形は、定義の補足（命題１ー３４）による。
• ここにおいて、
  　等しいとは
  　切り貼りして互いに重ね合わせることができること
  　ということが明確になった。
  

ＡＢＣＤ、ＥＢＣＦを
　同じ底辺ＢＣ上にあり
　かつ
　同じ平行線ＡＦ、ＢＣの間にある
　平行四辺形とせよ。

• 　線分ＢＣ
  に対して、
  　線分ＡＦ‖ＢＣ、
  　点Ｄ(ＡＦ;;ＡＤ＝ＢＣ)、
  　点Ｅ(ＡＦ;;ＥＦ＝ＢＣ)、
  　平行四辺形ＡＢＣＤ、ＥＢＣＦ
  をとる。
  

ＡＢＣＤは
　平行四辺形ＥＢＣＦに等しいと主張する。


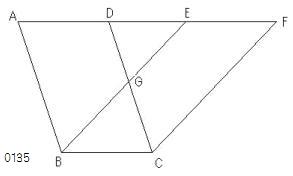
［Ｅが
　ＡＤの間にある場合と
　ＡＤの間にない場合とがある。
ＡＤの間にない場合について、］
ＡＢＣＤは
　平行四辺形であるから、
　ＡＤはＢＣに等しい。

• 命題の設定 ,
  命題１ー３４（平行四辺形の対辺・対角・対角線）
  による。
• 　ＡＤ＝ＢＣ
  となっている。

同じ理由で
　ＥＦもＢＣに等しい。
それゆえ
　ＡＤはまたＥＦに等しい。

• 公理１ー１（同じものに等しい）
  による。
• 　ＡＤ＝ＥＦ
  となっている。

そして
　ＤＥは共通である。
ゆえに
　ＡＥ全体はＤＦ全体に等しい。
　　　　　　【・・・(1)】

• 公理１ー２（等しいものに等しいものを加える）
  による。
• 　ＡＥ＝ＤＦ
  となっている。

しかも
　ＡＢはＤＣに等しい。

• 命題１ー３４（平行四辺形の対辺・対角・対角線）
  による。
• 　ＡＢ＝ＤＣ
  となっている。

かくて、
　２辺ＥＡ、ＡＢはＦＤ、ＤＣに等しい。

• (1) による。
• 　(ＥＡ,ＡＢ)＝(ＦＤ,ＤＣ)
  となっている。

そして
　角ＦＤＣは角ＥＡＢに、
　外角は内［対］角に等しい。

• 定義の補足（命題１ー２８）(外角･内対角(平行線))
  による。

ゆえに
　底辺ＥＢは
　底辺ＦＣに等しく、
　三角形ＥＡＢは
　三角形ＦＤＣに等しいであろう。

• 命題１ー４（２辺挟角相等）
  による。
• 　△ＥＡＢ≡△ＦＤＣ
  となっている。

双方から
　ＤＨＥが引き去られたとせよ。
　そうすれば
　残りの不等辺四辺形ＡＢＧＤは
　残りの不等辺四辺形ＥＧＣＦに等しい。

• 公理１ー３（等しいものから等しいものをひく）
  による。
• 等しいということが、
  　面積、
  　つまり
  　長さと幅とがかかわる広さに
  　関するものであることがわかる。
• 　四辺形ＡＢＧＤ＝四辺形ＥＧＣＦ
  となっている。

双方に
　三角形ＧＢＣが加えられたとせよ。
そうすれば
　平行四辺形ＡＢＣＤ全体は
　ＥＢＣＦ全体に等しい。

• 公理１ー２（等しいものに等しいものを加える）
  による。
• 　平行四辺形ＡＢＣＤ＝平行四辺形ＥＢＣＦ
  となっている。

よって
　同じ底辺の上にあり
　かつ
　同じ平行線の間にある
　平行四辺形は
　互いに等しい。

• Ｅが
  　ＡＤの間にある場合ついては、
  　共通なＤＥを引くことで、
  　三角形ＥＡＢとＦＤＣが
  　等しくなることが示され、
  　四角形ＤＢＣＡを双方に加えることで、
  　平行四辺形ＡＢＣＤとＥＢＣＦが
  　等しいことが示される。

これが証明すべきことであった。

• 面積の定義を明示的に与えず、
  　公理１ー７（等しい）、
  　公理１ー８（大きい）
  により、大小関係を論じている。
• 命題1-35は、
  　線分ＢＣ
  に対して、
  　線分ＡＦ‖ＢＣ、
  　点Ｄ(ＡＦ;;ＡＤ＝ＢＣ)、
  　点Ｅ(ＡＦ;;ＥＦ＝ＢＣ)、
  　平行四辺形ＡＢＣＤ、ＥＢＣＦ
  をとれば、
  　平行四辺形ＡＢＣＤ＝平行四辺形ＥＢＣＦ
  のことである。
• 命題1-35は推論用命題である。

  前提	作図	推論
  定義		補（題1-28）
  公準
  公理		1-1、1-2、1-3
  命題		1-4、1-34
  その他

前 　　 次 　　 目次 　　頁頭