ユークリッド原論をどう読むか(3)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1ー27(錯角と平行)
錯角
もし
1直線が2直線に交わってなす錯角が
互いに等しければ、
この2直線は互いに平行であろう。
- 直線は、定義1ー4による。
- 交わるは、定義1ー8の補足による。
- 錯角はここで初めて登場する。
1直線が2直線に交わっているとき、
2直線の内側にある四つの角のうち、
互いに同側内角でもなく接角でもない
二つの角を錯角という。
錯角は2組ある。
(以下、定義の補足(命題1ー27)(錯角)という。)
- 等しいは、公理1ー7による。
- 平行、定義1ー23による。
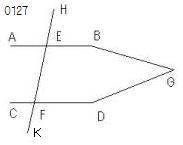
直線EFが
2直線AB、CDに交わり
錯角AEF、EFDを
互いに等しくするとせよ。
-
線分AB
に対して、
点E[AB]、
点F[外.AB]、
点D[反対側(EF,A);;∠EFD=∠AEF]、
点C[延長DF]
をとっている。
ABはCDに平行であると主張する。
もし平行でなければ、
AB、CDは延長されて
B、DまたはA、Cの側[と同じ側]で
交わるであろう。
[
B、Dと同じ側にある場合
]
延長され、
B、Dの側でGで交わるとせよ。
- B、Dの側で
交わる場合を考えるのである。
-
交点G(AB,CD);同側(EF,B)
となっている。
すると
三角形GEFにおいて
AEFが内対角EFGに等しい。
- 命題の設定 による。
-
∠AEF=∠EFG
となっている。
これは不可能である。
それゆえ
AB、CDは延長されて
B、Dの側で交わらないであろう。
- 背理法による。
-
延長AB¬╂延長CD
となっている。
[
A、Cと同じ側にある場合
]
同様にして
A、Cの側でも
交わらないことが証明されうる。
- A、Cの側でも交わる場合を
「同様にして」で済ませている。
-
延長BA¬╂延長DC
となっている。
そして
[
2つの場合より
]
どちらの側でも交わらない2直線は平行である。
したがって
ABはCDに平行である。
よってもし
1直線が
2直線に交わってなす錯角が
互いに等しければ、
この2直線は互いに平行であろう。
これが証明すべきことであった。
-
この命題
は、
公準1ー5(平行線公準)
の裏である次の
命題1ー28(内対角、同側内角と平行)
と同値である。
- 命題1-27は、
直線AB、CD、EF
について、
EF;(╂AB,╂CD)、
∠AEF=∠EFD、
ならば、
AB‖CD
のことである。
- 命題1-27は推論用命題である。
前
次
目次
頁頭
