ユークリッド原論をどう読むか（３）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー３３（等しく平行な２線分）
等しくかつ平行な２線分を
　同じ側で結ぶ２線分は
　それ自身等しくかつ平行である。

• 等しいは、公理１ー７による。
• 平行は、定義１ー２３による。
• 線分は、定義１ー４の補足による。
• 同じ側は、
  　定義１ー７の補足によるが、
  　ここでは、
  　平行な２線分の
  　それぞれの端点どうしを結んでできる２線分が、
  　その一方の線分について、
  　他方の線分が
  　すべて同じ側にあるという意味である。
  　つまり、
  　結んでできる２線分が
  　交わらないということである。

ＡＢ、ＣＤが
　等しくかつ平行であるとし、
　線分ＡＣ、ＢＤが
　それらを
　［つまり、
　線分ＡＣについて線分ＢＤを、
　線分ＢＤについて
　線分ＡＣを、］
　同じ側で結ぶとせよ。

• 　線分ＡＢ
  に対して
  　点Ｃ[外.ＡＢ]、
  　線分ＡＣ、
  　点Ｄ(平行線(Ｃ,ＡＢ),同側(ＡＣ,Ｂ);;ＣＤ＝ＡＢ)、
  　線分ＢＤ
  をとっている。

ＡＣ、ＢＤも等しくかつ平行であると主張する。
　

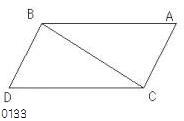
ＢＣが結ばれたとせよ。

• 公準１ー１（作図.直線）
  による。
• 　線分ＢＣ
  をとっている。

ＡＢはＣＤに平行であり、

• 命題の設定 による。
• 　ＡＢ‖ＣＤ
  となっている。

ＢＣはそれらに交わるから、
　錯角ＡＢＣ、ＢＣＤは互いに等しい。
　　　　　　【・・・(1)】

• 命題１ー２９（平行と錯角、内対角、同側内角）
  による。
• 　∠ＡＢＣ＝∠ＢＣＤ
  となっている。

そしてＡＢはＣＤに等しく、

• 命題の設定 による。
• 　ＡＢ＝ＣＤ
  となっている。

ＢＣは共通であるから、
　２辺ＡＢ、ＢＣは
　２辺ＢＣ、ＣＤに等しい。
また角ＡＢＣは角ＢＣＤに等しい。

• (1) による。
• 　(ＡＢ,ＢＣ)＝(ＢＣ,ＣＤ)、
  　∠ＡＢＣ＝∠ＢＣＤ
  となっている。

それゆえ
　底辺ＡＣは底辺ＢＤに等しく、
　三角形ＡＢＣは三角形ＢＣＤに等しく、
　残りの２角は残りの２角に等しい。
すなわち
　等しい辺が対する角はそれぞれ等しい。
　　　　　　【・・・(2)】

• 命題１ー４（２辺挟角相等）
  による。
• 　ＡＣ＝ＢＤ、
  　△ＡＢＣ≡△ＢＣＤ
  となっている。

そして
　２直線ＡＣ、ＢＤに
　線分ＢＣが交わり錯角を
　互いに等しくしているから、

• 　前節による。
• 　∠ＡＣＢ＝∠ＤＢＣ
  となっている。

　ＡＣはＢＤに平行である。

• 命題１ー２７（錯角と平行）
  による。
• 　ＡＣ‖ＢＤ
  となっている。

そして
　それに等しいことも先に証明された。

• (2) による。
• 　ＡＣ＝ＢＤ
  となっている。

よって
　等しくかつ平行な２線分を
　同じ側で結ぶ２線分は
　それ自身等しくかつ平行である。
　
これが証明すべきことであった。

• この命題は
  　平行四辺形について述べているのではない。
• 命題1-33は、
  　線分ＡＢ
  に対して、
  　線分ＣＤ‖ＡＢ、
  　ＣＤ＝ＡＢ、
  　Ｄ;同側(ＡＣ,Ｂ)、
  　線分ＡＣ、ＢＤ
  をとれば、
  　ＡＣ＝ＢＤ、
  　ＡＣ‖ＢＤ
  のことである。　
• 命題1-33は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理
  命題		1-4、1-27、1-29
  その他

前 　　 次 　　 目次 　　頁頭