ユークリッド原論をどう読むか（１６）
頁末 　　 前 　　 次 　 目次

ユークリッド原論

第１１巻
　
命題１１ー１１（作図.平面への垂線）
　　面外の与えられた点から
　　　与えられた平面へ垂直な直線を
　　ひくこと。

• 面は、
  定義１ー５による。
• 点は、
  定義１ー１による。
• 平面は、
  定義１ー７による。
• 垂直は、
  定義１ー１０の補足２による。
• 直線は、
  定義１ー４による。

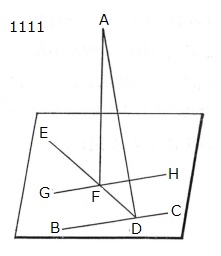
　　面外の与えられた点をＡとし，
　　与えられた平面を基準平面とせよ。
このとき
　　　点Ａから基準平面へ
　　垂直な直線をひかねばならぬ。

　基準平面上に任意に線分ＢＣが
　　ひかれ，
　　点ＡからＢＣへ垂線ＡＤがひかれた
とせよ。
　　　　[......(１)]

• 　公準１ー１の補足２（作図.任意の線分・直線をひく）、
  　命題１１ー２の補足(作図.交わる２直線、１直線上にない３点、１直線とその上にない１点で平面が決定)、
  　命題１ー１２（作図・線分への垂線）
  による。
• 　ＢＣ（基準平面；）、
  　Ｄ（ＢＣ；ＡＤ⊥ＢＣ）
  となっている。

そうすれば
"case01"
"case02"
"case0e"
"case01"
もし
　ＡＤが
　　基準平面に対しても垂直である
ならば，
　命じられたことは
　　なされているであろう。
"case01end"

• 　場合分けのケース１である。
  　ケース１では、
  　　それで、作図終了である。
• 　ＡＤ⊥基準平面
  となっている。

"case02"
ところが
もし
そうでないならば，

• 　場合分けのケース２である。
• 　ＡＤ⊥ＢＣ、
  　ＡＤ¬⊥基準平面
  となっている。

　　　点ＤからＢＣに
　　　直角に基準平面上に
　ＤＥが
　　ひかれ，
　　　ＡからＤＥに
　垂線ＡＦが
　　下され，
　　　点Ｆを通りＢＣに平行に
　ＧＨが
　　ひかれたとせよ。
　　　　[......(２)]

• 　命題１ー１１（作図・線分からの垂線）、
  　命題１ー３１（作図・平行線）
  による。
• 　Ｅ（基準平面；ＤＥ⊥ＢＣ）、
  　Ｆ（ＤＥ；ＡＦ⊥ＤＥ）、
  　Ｇ、Ｈ（基準平面；ＧＦ、ＦＨ‖ＢＣ）
  となっている。

そうすれば
　ＢＣは
　　ＤＡ、ＤＥの双方に垂直である
から，
　ＢＣは
　　　ＥＤ、ＤＡを通る平面に対しても
　　垂直である。

• 　（１） （２）、
  　命題１１ー４（交わる２直線に垂直な直線はそれらを通る平面にも垂直）
  による。
• 　ＢＣ⊥平面（ＥＤ、ＤＡ）
  となっている。

そして
　ＧＨは
　　それに平行である。

• 　前々節による。
• 　ＧＨ‖ＢＣ
  となっている。

ところで
もし
　２直線が
　　平行であり，
　それらの一方が
　　ある平面に垂直である
ならば，
　残りの直線も
　　同じ平面に垂直であろう。

• 　命題１１ー８（平行線の一方が平面に垂直なら他方も垂直）
  による。

それゆえ
　ＧＨも
　　ＥＤ、ＤＡを通る平面に直角である。

• 　前節、前々節
  による。
• 　ＧＨ⊥平面（ＥＤ、ＤＡ）
  となっている。

ゆえに
　ＧＨは
　　それと会し
　　かつ
　　　ＥＤ、ＤＡを通る平面上の
　　　すべての直線に対しても
　　垂直である。

• 　前節、
  　定義１１ー３（直角(直線・平面)）
  による。
• 　ＧＨ⊥直線（平面（ＥＤ、ＤＡ）；（交わる）ＧＨ）
  となっている。

ところが
　ＡＦは
　　それと会し
　　かつ
　　ＥＤ、ＤＡを通る平面上にある。

• 　（２）
  による。
• 　ＡＦ；（交わる）ＧＨ、平面（ＥＤ、ＤＡ）上
  となっている。

したがって
　ＧＨは
　　ＦＡに対し垂直である。

• 　前節、前々節
  による。
• 　ＧＨ⊥ＦＡ
  となっている。

それゆえ
　ＦＡも
　　ＨＧに直角である。

• 　前節
  による。
• 　ＦＡ⊥ＨＧ
  となっている。

しかも
　ＡＦは
　　ＤＥにも垂直である。

• 　（２）
  による。
• 　ＡＦ⊥ＤＥ
  となっている。

ゆえに
　ＡＦは
　　ＧＨ、ＤＥの双方に垂直である。

• 　前節、前々節
  による。
• 　ＡＦ⊥ＧＨ、ＤＥ
  となっている。

ところが
もし
　一つの直線が
　　　互いに交わる２直線に対し
　　　それらの交点において
　　垂直に立てられた
ならば，
　　　それらを通る平面に対しても
　　垂直であろう。

• 　命題１１ー４（交わる２直線に垂直な直線はそれらを通る平面にも垂直）
  による。

したがって
　ＦＡは
　　　ＥＤ、ＧＨを通る平面に対し
　　垂直である。

• 　前節、前々節
  による。
• 　ＦＡ⊥平面（ＥＤ、ＧＨ）
  となっている。

ところが
　ＥＤ、ＧＨを通る平面は
　　基準平面である。

• 　（２）
  による。
• 　平面（ＥＤ、ＧＨ）；基準平面
  となっている。

ゆえに
　ＡＦは
　　基準平面に垂直である。

• 　前節、前々節
  による。
• 　ＡＦ⊥基準平面
  となっている。

"case0e"
よって
　　　面外の与えられた点Ａから
　基準平面へ垂直な線分ＡＦが
　　ひかれた。
これが作図すべきものであった。

• 命題１１ー１１は、
  　三垂線の定理のことで、
  　基準面外のＡから、
  　基準面への垂線をとる
  には、
  　基準面に直線ＢＣをとり、
  　ＡからＢＣに垂線ＡＤをとり、
  　基準面上で
  　ＤからＢＣとの垂線ＤＥをとり、
  　ＡからＤＥへの垂線ＡＦをとれば、
  　ＡＦは基準面への垂線
  のことである。
• 命題１１ー１１は作図用命題である。

  前提	作図・構成	推論
  定義		11-3
  公準	1-1補2
  公理
  命題	1-11,1-12,1-31,11-2補2	11-4,11-8
  その他		場合分け

前 　　 次 　　 目次 　　頁頭