ユークリッド原論をどう読むか（１６）
頁末 　　 前 　　 次 　 目次

ユークリッド原論

第１１巻
　
命題１１ー１２（作図.平面上の点から垂線）
　　　与えられた平面に対し
　　　その上の与えられた点から
　　垂直に直線をたてる
こと。

• 平面は、
  定義１ー４による。
• 点は、
  定義１ー１による。
• 垂直は、
  定義１ー１０の補足２による。
• 直線は、
  定義１ー４による。

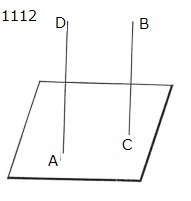
　　与えられた平面を基準平面とし，
　　Ａをその上の点とせよ。

• 　公準の補足２（命題１１ー２）(作図.空間に任意の平面をとる)、
  　公準１ー１の補足（作図.任意の点をとる）
  による。
• 　Ａ；基準平面上
  となっている。

このとき
　　　点Ａから基準平面に垂直に
　　直線をたてねばならぬ。


　面外の任意の点Ｂが
　　考えられ，
　　　Ｂから基準平面へ
　垂線ＢＣが
　　下されたとし，
そして
　　　点Ａを通りＢＣに平行に
　ＡＤが
　　ひかれたとせよ。

• 　公準１ー１の補足（作図.任意の点をとる）、
  　命題１１ー１１（作図.平面への垂線）、
  　命題１１ー７の補足(作図.空間に平行線)
  による。
• 　Ｂ（基準平面外；）、
  　Ｃ（基準平面；ＢＣ⊥）、
  　Ｄ（基準平面外；ＡＤ‖ＢＣ）
  となっている。

そうすれば
　ＡＤ、ＣＢは
　　二つの平行線であり，
　それらの一方ＢＣは
　　基準平面に垂直である

• 　前節による。
• 　ＡＤ‖ＣＢ、
  　ＢＣ⊥基準平面
  となっている。

から，
　残りの線分ＡＤも
　　基準平面に垂直である。

• 　前節、
  　命題１１ー８（平行線の一方が平面に垂直なら他方も垂直）
  による。
• 　ＡＤ⊥基準平面
  となっている。

よって
　　　与えられた平面に対し
　　　その平面上の点Ａから垂直に
　ＡＤが
　　立てられた。
これが作図すべきものであった。

• 命題１１ー１２は、
  　　　基準平面外の点から
  　　基準平面に垂線をおろし、
  　　　基準平面上の点から、
  　　その垂線に平行な直線をとることで、
  　　　基準平面上の点から、
  　　基準平面に垂直な直線をとる
  ことである。
• 命題１１ー１２は作図用命題である。

  前提	作図・構成	推論
  定義
  公準	1-1補,1-1補2,補2(題11-2)
  公理
  命題	11-7補,11-11	11-8
  その他

前 　　 次 　　 目次 　　頁頭