ユークリッド原論をどう読むか(16)
頁末
前
次
目次
ユークリッド原論
第11巻
命題11ー10(相会する2直線が相会する2直線に平行なら等しい角をはさむ)
もし
相会する2直線が,
同じ平面上にない
相会する2直線に平行である
ならば,
それらは
等しい角をはさむであろう。
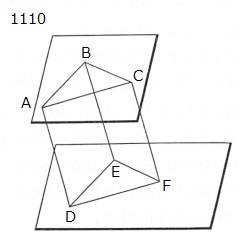
相会する2直線AB、BCが、
同じ平面上にない
相会する2直線DE、EFに平行である
とせよ。
-
公準の補足2(命題11ー2) (作図.空間に任意の平面をとる)
により、
平面P1をとり、
公準1ー1の補足(作図.任意の点をとる)
により、
平面上に点A、Bをとり、
公準1ー1(作図.直線)
により、
直線ABをとり、
公準1ー1の補足(作図.任意の点をとる)
により、
AB外に点Cをとり、
公準1ー1(作図.直線)
により、
直線BCをとる。
公準1ー1の補足(作図.任意の点をとる)
により、
P1外に点Eをとり、
命題11ー2の補足(作図.交わる2直線、1直線上にない3点、1直線とその上にない1点で平面が決定)
により、
AB、Eを通る平面P2、
BC、Eを通る平面P3をとり、
命題1ー31(作図・平行線)
により、
P2上にEを通り、ABに平行な直線DE、
P3上にEを通り、BCに平行な直線EFをとる。
-
DE、EF;平面(AB、BC)外
AB‖DE、
BC‖EF
となっている。
角ABCは
角DEFに等しい
と主張する。
[......(1)]
BA、BC、ED、EFが
互いに等しく切りとられ,
AD、CF、BE、AC、DFが
結ばれた
とせよ。
-
命題1ー3(作図・等しい線分を切り取る)、
公準1ー1(作図.直線)
による。
改めて、
A、C、D、F
をとっている。
-
AB=BC=ED=EF
となっている。
そうすれば
BAは
EDに等しく平行である
から,
ADも
BEに等しく平行である。
-
前節、
命題1ー33(等しく平行な2線分)
による。
-
AD=BE、
AD‖BE
となっている。
同じ理由で
CFも
BEに等しく平行である。
-
前々節、
命題1ー33(等しく平行な2線分)
による。
-
CF=BE、
CF‖BE
となっている。
それゆえ
AD、CFの双方は
BEに等しく平行である。
-
前節、前々節、
による。
-
AD、CF=BE、
AD、CF‖BE
となっている。
ところが
同一直線に平行であり,
それと同じ平面上にない
二つの直線は
互いにも平行である。
ゆえに
ADは
CFに平行で等しい。
-
前節、
公理1ー1(同じものに等しい)、
による。
-
AD=CF、
AD‖CF
となっている。
そして
AC、DFが
それらを結ぶ。
したがって
ACは
DFに等しく平行である。
-
前節、
命題1ー33(等しく平行な2線分)
による。
-
AC=DF、
AC‖DF
となっている。
そして
2辺AB、BCは
2辺DE、EFに等しく,
底辺ACも
底辺DFに等しい
から,
角ABCは
角DEFに等しい。
-
(1)、前節
命題1ー8(3辺相等2)
による。
-
∠ABC=∠DEF
となっている。
よって
もし
相会する2直線が,
同じ平面上にない
相会する2直線に平行である
ならば,
それらは
等しい角をはさむであろう。
これが証明すベきことであった。
- 命題11ー10は、
DE、EF;平面(AB、BC)外、
AB=BC=DE=EF、
AB‖DE、
BC‖EF
なら、
AD=BE=CF、
AD‖BE‖CF
となり、
AC=DF
となって、
△ABC≡△DEF
となって、
∠ABC=∠DEF
のことである。
- 命題11ー10は推論用命題である。
前
次
目次
頁頭
