ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第１０巻
　
命題１０ー３７（平方でのみ通約で有理面積をかこむ中項線分和は第１双中項線分）
第１の双中項線分
もし 　平方においてのみ通約でき，
　　有理面積をかこむ二つの中項線分
　　が加えられる
ならば，
　全体は無理線分であり，
　そして
　第１の双中項線分
とよばれる。

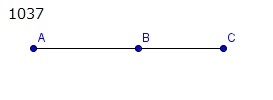
• 平方においてのみ通約は、
  定義の補足（命題１０ー１９助）による。
• 有理面積は、
  定義１０ー４の補足による。
• 中項線分は、
  定義の補足（命題１０ー２１）による。
• 無理線分は、
  定義１０ー４による。
• 第１の双中項線分は、
  　平方においてのみ通約でき、
  　　有理面積をかこむ二つの中項線分の和
  のことをいう。
  (以下、定義の補足(命題１０ー３７) (第１双中項線分)という。)
  

　平方においてのみ通約でき，
　　有理面積をかこむ二つの
　　中項線分ＡＢ，ＢＣ
　　が加えられたとせよ。
　ＡＣ全体は
　　無理線分である
と主張する。

• 　命題１０ー２７（作図.２中項線分;矩形が有理面積、平方でのみ通約）
  による。
  
• 　中項線分ＡＢ,ＢＣ；
  　　,ＡＢ∩^^2 ＢＣ
  　　,矩形(ＡＢ,ＢＣ)；有理面積）
  をとっている。

　ＡＢは
　　ＢＣと長さにおいて通約できない

• 　命題の設定による。
• 　ＡＢ¬∩ ＢＣ
  となっている。

から，
　ＡＢ，ＢＣ上の正方形の和は
　　矩形ＡＢ，ＢＣの２倍
　と通約できない。

• 　命題１０ー２２助（２線分は一方の上の正方形と両者の矩形に比例）
  により、
  　矩形(ＡＢ,ＢＣ)：正方(_ＡＢ)＝ＢＣ：ＡＢ、
  　矩形(ＡＢ,ＢＣ)：正方(_ＢＣ)＝ＡＢ：ＢＣ、
  となり、
  　前節、
  　命題１０ー１１（４量比例で一方が通約なら他方も通約）、
  　命題１０ー１６（非通約量はその和・差とも非通約） による。　
  
• 　正方(_ＡＢ) +正方(_ＢＣ)¬∩矩形(ＡＢ,ＢＣ)
  となっている。

そして
合比により
　ＡＢ，ＢＣ上の二つの正方形
　と矩形ＡＢ，ＢＣの２倍との和，
　すなわち
　ＡＣ上の正方形は
　　矩形ＡＢ，ＢＣ
　と通約できない。

• 　前節、
  　命題１０ー１６（非通約量はその和・差とも非通約）
  による。
• 　正方(_ＡＣ)¬∩矩形(ＡＢ,ＢＣ)
  となっている。

ところが
　ＡＢ，ＢＣは
　　有理面積をかこむ線分
　　であると仮定される
から，
　矩形ＡＢ，ＢＣは
　有理面積である。

• 　命題の設定である。
• 　矩形(ＡＢ,ＢＣ)；有理面積
  となっている。

したがって
　ＡＣ上の正方形は
　　無理面積である。

• 　前節、
  　定義１０ー４の補足 （有理面積、無理面積）
  による。
• 　正方(_ＡＣ)；無理面積
  となっている。

よって
　ＡＣも無理線分であり，

• 　前節、
  　定義１０ー４（面積の有理、無理、無理線分）
  による。
• 　ＡＣ；無理線分
  となっている。

　そして
　第１の双中項線分
　とよばれる。

• 　前節、
  　定義の補足(命題１０ー３７) (第一双中項線分)
  による。
• 　ＡＣ；第１の双中項線分
  となっている。

これが証明すべきことであった。

• 命題１０ー３７は、
  　命題１０ー２７ により、
  　　中項線分ＡＢ,ＢＣ；
  　　,ＡＢ∩^^2 ＢＣ
  　　,矩形(ＡＢ,ＢＣ)；有理面積）
  をとれば、
  　ＡＣ＝ＡＢ＋ＢＣ：第一双中項線分
  のことである。
• 命題１０ー３７は推論用命題である。

  前提	作図・構成	推論
  定義		10-4,10-4補,補(題10-37)
  公準
  公理
  命題	10-27	10-11,10-16,10-22助
  その他

前 　　 次 　　 目次 　　頁頭