ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第１０巻
　
命題１０ー２２助（２線分は一方の上の正方形と両者の矩形に比例）

　補　助　定　理

もし
　２つの線分がある
ならば、
　第１が第２に対するように、
　第１の上の正方形が
　これらの２線分によって
　かこまれる矩形に対する。

• 線分は、
  定義の補足（命題１ー１）による。
• 対する・ようには、
  定義の補足３（命題５ー１１）による。
• 正方形・矩形は、
  定義１ー２２による。

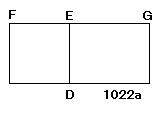
　２線分ＦＥ、ＥＧがある
とせよ。

• 　公準１ー１の補足２（作図.任意の線分）
  により、
  　２線分ＥＦ、ＥＧをつくる。

　ＦＥがＥＧに対するように、
　ＦＥ上の正方形が矩形ＦＥ、ＥＧに対する
と主張する。

　ＦＥ上に正方形ＤＦが描かれ、
　ＧＤが完結された
とせよ。

• 　命題１−４６（作図.線分上に正方形）
  による。
  
• 　「［平行四辺形の］完結」は、
  　コメント２（命題６ー１４）
  　参照のこと。
• 　sq(ＤＦ)＝sq(_ＦＥ)
  となっている。

そうすれば
　ＦＥがＥＧに対するように、
　ＦＤがＤＧに対し、

• 　前節、
  　命題６ー１（同高の三角形、平行四辺形は底辺と比例）
  による。
  
• 　ＦＥ：ＥＧ＝sq(ＦＤ)：rec(ＤＧ)
  となっている。

　ＦＤはＦＥ上の正方形であり、

• 　前々節による。
• 　sq(ＦＤ)＝sq(_ＦＥ)
  となっている。

　ＤＧは矩形ＤＥ、ＥＧ、
　すなわち
　矩形ＦＥ、ＥＧである

• 　rec(ＤＧ)＝rec(ＦＥ、ＥＧ)
  となっている。

から、
　ＦＥがＥＧに対するように、
　ＦＥ上の正方形が矩形ＦＥ、ＥＧに対する。

• 　前節、前々節、前々々節、
  　命題５ー７（同一量の比）
  による。
• 　ＦＥ：ＥＧ＝sq(_ＦＥ)：rec(ＦＥ、ＥＧ)
  となっている。

同様にして
　矩形ＧＥ、ＥＦがＥＦ上の正方形に対する、
　すなわち
　ＧＤがＦＤに対するように、
　ＧＥがＥＦに対する。

• 　前節によれば、
  　命題５ー７の系(比例すれば逆も比例)、
  　命題５ー１１の補足（同じ比は互いに同じ）
  による。
  
• 　本命題に即していえば、
  「　これらの２線分によって
  　かこまれる矩形が
  　第１の上の正方形に対するように、
  　第２が第１に対する。」
  ということである。
• 　本命題にとっては、
  　蛇足である。
  

　これが証明すべきことであった。

• 命題１０ー２２助は、
  　Ａ：Ｂ＝sq(_Ａ)：rec(Ａ、Ｂ)
  のことである。
  
  
• 命題１０ー２２助は推論用命題である。

  前提	作図・構成	推論
  定義
  公準	1-1補2
  公理
  命題		5-7,5-7系,5-11補,6-1
  その他	コ2(題6-14)

前 　　 次 　　 目次 　　頁頭