ユークリッド原論をどう読むか(14)
頁末
前
次
目次
ユークリッド原論
第10巻
命題10ー16(非通約量はその和・差とも非通約)
もし
2つの通約できない量が加えられる
ならば、
全体もそれらの双方と通約できない
であろう。
そして
もし
全体がそれらの一方と通約できない
ならば、
最初の2量も通約できない
であろう。
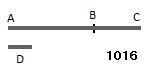
2つの通約できない量
AB、BCが加えられた
とせよ。
-
「量(について)・・・とせよ」は、
コメント6(命題5ー1)
参照のこと。
-
命題10ー10
(作図.長さ・平方において通約でない線分)
により、
AB、BCをとる。
-
AB¬∩BC
となっている。
AC全体も
AB、BCの双方と通約できない
と主張する。
もし
CA、ABが通約できなくない
ならば、
何らかの量がそれらを割り切る
であろう。
もし可能ならば、
割り切る
とし、
それをD
とせよ。
-
背理法の仮定である。
-
「もし可能ならば」は、
コメント2(命題1−7)
参照のこと。
-
D|CA、D|AB
となっている。
そうすれば
DはCA、ABを割り切る
から、
残りのBCをも割り切る
であろう。
そして
ABをも割り切る。
したがって
DはAB、BCを割り切る。
-
前節、前々節による。
-
D|AB、D|BC
となっている。
それゆえ
AB、BCは通約できる。
ところが
通約できない
と仮定された。
これは不可能である。
したがって
いかなる量も
CA、ABを割り切らない
であろう。
ゆえに
CA、ABは通約できない。
同様にして
AC、CBも通約できない
ことを証明しうる。
したがって
ACはAB、BCの双方と通約できない。
-
前節、前々節による。
-
AC¬∩AB、AC¬∩BC
となっている。
次に
ACがAB、BCの一方と
通約できない
とせよ。
まず
ABと通約できない
とせよ。
[......(a)]
AB、BCも通約できない
と主張する。
もし
通約できる
ならば、
何らかの量がそれらを割り切る
であろう。
割り切る
とし、
それをD
とせよ。
-
背理法の仮定である。
-
D|AB、D|BC
となっている。
そうすれば
DはAB、BCを割り切る
から、
AC全体をも割り切る
であろう。
そして
ABをも割り切る。
したがって
DはCA、ABを割り切る。
-
前節、前々節による。
-
D|CA、D|BC
となっている。
それゆえ
CA、ABは通約できる。
ところが
通約できない
と仮定された。
これは不可能である。
したがって
いかなる量も
AB、BCを割り切らない
であろう。
ゆえに
AB、BCは通約できない。
-
前節、
定義10ー1(通約)
による。
-
AB¬∩BC
となっている。
[次に、
ACがBCと通約できない
としても、
同様にして
AB、BCは通約できない
ことを証明しうる。]
よって
もし
2つの[通約できない]量が云々
-
云々は
「加えられる
ならば、
全体もそれらの双方と通約できない
であろう。
そして
もし
全体がそれらの一方と通約できない
ならば、
最初の2量も通約できない
であろう。」
-
命題10ー16は、
A¬∩B
ならば、
A十B¬∩A、A+B¬∩B
およびその逆
A+B¬∩A
ならば、
A¬∩B
のことである。
- 命題10ー16は推論用命題である。
前
次
目次
頁頭
