ユークリッド原論をどう読むか（９502）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー２（同数倍の和２）
（倍量の和は倍量）
第１の量が第２の、
　第３が第４の
　　同数倍であり、
　第５が第２の、
　第６が第４の
　　同数倍であるならば、
　第１と第５の和が第２の、
　第３と第６の和が第４の
　　同数倍であろう。

• 量は、定義５ー１の補足 による。
• 同数倍は、定義５ー５の補足 による。
• 初めの２つの同数倍は、
  　それぞれ独立である。
  すなわち、
  　異なる個数である。
  ３つめの同数倍は、
  　初めの２つの同数倍（個数）の和である。

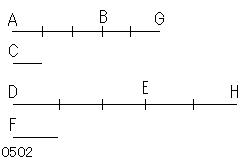
第１の量ＡＢが第２のＣの、
　第３のＤＥが第４のＦの
　　同数倍であるとし、
　そして
　第５のＢＧが第２のＣの、
　第６のＥＨが第４のＦの
　　同数倍であるとせよ。

• 　ＡＢ＝ｍＣ、
  　ＤＥ＝ｍＦ、
  　ＢＧ＝ｎＣ、
  　ＥＨ＝ｎＦ
  をとっている。

第１と第５の和ＡＧが第２のＣの、
　第３と第６の和ＤＨが第４のＦの
　　同数倍である
　と主張する。

• 量の倍は、
  命題の補足（定義５ー２）（作図.倍量）、
  量の和は、
  命題の補足（定義５ー１４）（作図.量の和）
  による。

ＡＢがＣの、
　ＤＥがＦの
　　同数倍であるから、

• 命題の設定 による。
• 　ＡＢ＝ｍＣ、
  　ＤＥ＝ｍＦ
  となっている。

　ＡＢのなかにある
　　Ｃに等しい量と同数の、
　　Ｆに等しい量が
　ＤＥのなかにある。【・・・(1)】

• 定義５ー５の補足（同数倍）
  による。
• 　個数(ＡＢ,Ｃ)＝個数(ＤＥ,Ｆ)＝ｍ
  となっている。

同じ理由で
　ＢＧのなかにある
　　Ｃに等しい量と同数の、
　　Ｆに等しい量が
　ＥＨのなかにある。【・・・(2)】

• 　個数(ＢＧ,Ｃ)＝個数(ＥＨ,Ｆ)＝ｎ
  となっている。

それゆえ
　ＡＧ全体のなかにある
　　Ｃに等しい量と同数の、
　　Ｆに等しい量が
　ＤＨ全体のなかにある。

• (1) (2) 、
  公理の補足３（命題５ー１）(１対１対応)
  による。
• 　個数(ＡＧ,Ｃ)＝個数(ＤＨ,Ｆ)＝ｍ＋ｎ
  すなわち、
  　ＡＧ＝(ｍ＋ｎ)Ｃ、
  　ＤＨ＝(ｍ＋ｎ)Ｆ
  となっている。

ゆえに
　ＡＧがＣの何倍《であ》［にな］ろうと、
　ＤＨも
　Ｆの同じ倍数であろう。

• 定義の補足（命題５ー１）(同じ倍数)
  による。
• 　個数(ＡＧ,Ｃ)＝個数(ＤＨ,Ｆ)＝ｍ＋ｎ
  ということである。

したがって
　第１と第５の和ＡＧが
　第２のＣの、
　第３と第６の和ＤＨが
　第４のＦの
　　同数倍であろう。

• 定義５ー５の補足（同数倍）
  による。
• 　個数(ｍＣ＋ｎＣ,Ｃ)＝個数(ｍＦ＋ｎＦ,Ｆ)
  ということである。

よってもし
　第１の量が第２の、
　第３が第４の
　　同数倍であり、
　第５が第２の、
　第６が第４の
　　同数倍であるならば、
　第１と第５の和が
　第２の、
　第３と第６の和が
　第４の
　　同数倍であろう。
　 これが証明すべきことであった。

• 命題５ー２は、 個数(ｍＣ＋ｎＣ,Ｃ)＝個数(ｍＦ＋ｎＦ,Ｆ)＝ｍ＋ｎのことである。
  したがって、
  　 小さい量（基準とする大きさ）が何であろうと、
  　それについて
  　任意の倍量と別の任意の倍量との和は、
  　定義５ー２（倍量）
  により、
  　倍量である。
  （以下、命題５ー２の補足（倍量の和は倍量）という。）
  ｍＣ＋ｎＣ＝（ｍ＋ｎ）Ｃのことである。
• 命題５ー２の補足（倍量の和は倍量）

  前提	作図	推論
  定義		5-2
  公準
  公理
  命題		5-2
  その他

• 命題５ー２は推論用命題である。

  前提	作図	推論
  定義		5-5補,補(題5-1)
  公準
  公理		補3(題5-1)
  命題	補(義5-2),補(義5-14)
  その他

前 　　 次 　　 目次 　　頁頭