ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第１０巻
　
命題１０ー１７助（線分の矩形分割（コ））

　補　助　定　理
もし
　ある線分上に
　正方形だけ欠けている
　平行四辺形がつくられる
ならば、
　つくられた平行四辺形は
　その結果生ずる
　線分の２つの部分によってかこまれた
　矩形に等しい。

• 線分は、
  定義の補足（命題１ー１）による。
• 正方形は、
  定義１ー２２による。
• 平行四辺形は、
  定義１ー２２の補足による。
• かこまれるは、
  定義２ー１による。
• 矩形は、
  定義１ー２２による。

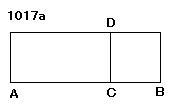
　線分ＡＢ上に
　正方形ＤＢだけ欠けている
　平行四辺形ＡＤがつくられた
とせよ。

• 　公準１ー１の補足（作図.点）
  により、
  　線分ＡＢ上に点Ｃをとり、
  　命題１−４６（作図.線分上に正方形）
  により、
  　ＢＣ上に正方形ＤＢをかく。
  
  　命題１ー３４の補足４（作図.隣り合う２辺から平行四辺形）
  により
  　平行四辺形ＡＤをかく。
  　ＡＤは結果的には矩形になる。

　ＡＤは矩形ＡＣ、ＣＢに等しい
と主張する。

　これは直ちに明らかである。

なぜなら
　ＤＢは正方形である

• 　命題の設定による。

から、
　ＤＣはＣＢに等しく、

• 　前節、
  　定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　ＤＣ＝ＣＢ
  となっている。

　ＡＤは
　矩形ＡＣ、ＣＤ、
　すなわち
　矩形ＡＣ、ＣＢである
から。

• 　前節、
  　定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　ＡＤ＝矩形ＡＣ、ＣＤ
  　＝矩形ＡＣ、ＣＢ
  となっている。

よって
もし
　ある線分上に云々

• 　云々は 「正方形だけ欠けている
  　平行四辺形がつくられる
  ならば、
  　つくられた平行四辺形は
  　その結果生ずる
  　線分の２つの部分によってかこまれた
  　矩形に等しい。」
  である。

• 命題１０ー１７助は推論用命題である。

  前提	作図・構成	推論
  定義		1-22
  公準	1-1補
  公理
  命題	1-34補,1-46
  その他

前 　　 次 　　 目次 　　頁頭