ユークリッド原論をどう読むか（１３）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第９巻
　
命題９ー３０（奇数が偶数整除なら半分も整除）
もし
　奇数が偶数を割り切る
ならば、
　その半分をも割り切る
であろう。

• 奇数は、
  定義７ー７による。
• 偶数は、
  定義７ー６による。
• 割り切るは、
  定義５ー１の補足２による。
• 半分は、
  定義の補足（公理１ー６）による。

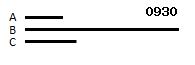
　奇数Ａが偶数Ｂを割り切る
とせよ。

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
  
• 　Ａ＝奇数、Ｂ＝偶数、
  　Ａ｜Ｂ
  となっている。
  

　その半分をも割り切る
であろうと主張する。

　ＡがＢを割り切る

• 　命題の設定による。
• 　Ａ｜Ｂ
  となっている。

から、
　その商をＣとせよ。
　　　　　　[......(ａ)]

• 　Ｂ／Ａ＝Ｃ
  となっている。

　Ｃは奇数でない
と主張する。

もし可能ならば、

• 　「もし可能ならば」は、
  　コメント２(命題１−７）
  　参照のこと。
  
• 　背理法の仮定を述べようとしている。

　奇数である
とせよ。

• 　背理法の仮定である。
• 　Ｃ＝奇数
  としている。

そうすれば
　ＡがＢを割った商はＣである

• 　（ａ）による。

から、
　ＡはＣにかけてＢをつくった。

• 　前節、
  　命題の補足４（定義７ー１６）（商を割る数にかけると割られる数）
  による。
  
• 　Ａ×Ｃ＝Ｂ
  となっている。
  

それゆえ
　Ｂは奇数個の奇数からなる。

• 　前節
  　定義７ー１６（かける）
  による。
  

ゆえに
　Ｂは奇数である。

• 　前節、
  　命題９ー２３（奇数の奇数和は奇数）
  による。
  

　これは不合理である。

なぜなら
　偶数である
と仮定されているから。

• 　「なぜなら・・・であるから」は、
  　コメント２（命題１ー１６）
  　参照のこと
  
• 　命題の設定による。

したがって
　Ｃは奇数ではない。

• 　背理法による。

ゆえに
　Ｃは偶数である。

• 　Ｃ＝偶数
  となっている。

よって
　ＡがＢを割った商は偶数である。

• 　前節、 （ａ）による。

このゆえに
　その半分をも割り切る
であろう。

• 　この証明は、以下のとおり。
  
  　前々節により
  　Ｃは偶数である
  から
  　Ｃ／２＝Ｄ
  とすると、
  　Ｄ＋Ｄ＝Ｃ
  となる。
  　Ａ×Ｄ＝Ｅ
  とすると、
  　Ａ｜Ｅ　・・・（ア）
  である。
  ところが、
  　Ａ×Ｄ＋Ａ×Ｄ
  　は、
  　命題５ー１（同数倍の和１）
  により、
  　Ａ×（Ｄ＋Ｄ）
  　＝Ａ×Ｃ
  　＝Ｂ
  となるので、
  　ＥはＢの半分である。
  　これと、（ア）により
  　ＡはＢの半分を割り切る。
  

これが証明すべきことであった。

• 命題９ー３０は、
  　Ａ；奇数、
  　Ｂ；偶数
  のとき、
  　Ａ｜Ｂ
  ならば、
  　Ａ｜Ｂ／２
  のことである。
• 命題９ー３０は推論用命題である。

  前提	作図	推論
  定義		7-16
  公準
  公理
  命題		5-1,補4(義7-16),9-23
  その他	コ4(題7-1)	コ2(題1-7),コ2(題1-16),背理法

前 　　 次 　　 目次 　　頁頭