ユークリッド原論をどう読むか（１３）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第９巻
　
命題９ー２９（奇数×奇数は奇数）
もし
　奇数が奇数にかけて
　ある数をつくる
ならば、
　その積は奇数
であろう。

• 奇数は、
  定義７ー７による。
• かけるは、
  定義７ー１６による。
• 数は、
  定義７ー２による。
• 積は、
  定義７ー１６の補足２による。

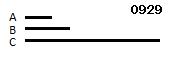
　奇数Ａが奇数Ｂにかけて
　Ｃをつくる
とせよ。

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
  
• 　Ａ、Ｂ＝奇数、
  　Ａ×Ｂ＝Ｃ
  となっている。
  

　Ｃは奇数である
と主張する。

　ＡはＢにかけてＣをつくった
から、
　ＣはＡのなかにある単位と同じ個数の、
　Ｂに等しい数から成る。

• 　前節、
  　定義７ー１６（かける）
  による。
  
• 　Ｃ＝Ｂ＋Ｂ＋・・・＋Ｂ（Ａ個）
  　Ａ、Ｂ＝奇数 となっている。
  

そして
　Ａ、Ｂの双方は奇数である。

それゆえ
　Ｃは奇数個の奇数から成る。

• 　前節、前々節による。

したがって
　Ｃは奇数である。

• 　前節、
  　命題９ー２３（奇数の奇数和は奇数）
  による。
  

　これが証明すべきことであった。

• 命題９ー２９は、
  　Ａ、Ｂ；奇数、
  のとき、
  　Ａ×Ｂ；奇数
  のことである。
  
• 命題９ー２９は推論用命題である。

  前提	作図	推論
  定義		7-16
  公準
  公理
  命題		9-23
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭