ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー３０（素数は積を割り切れば一方を割り切る）
もし
　２つの数が
　互いにかけあわせてある数をつくり、
　２数の積を何らかの素数が割り切る
ならば、
　それは
　最初の２数の１つをも
　割り切る
であろう。

• 数は、 定義７ー２による。
• かけるは、 定義７ー１６による。
• 積は、 定義７ー１６の補足２による。
• 素数は、 定義７ー１２による。
• 割り切るは、 定義５ー１の補足２による。

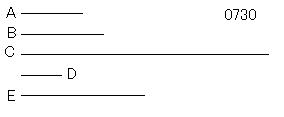
　２数Ａ、Ｂが
　互いにかけあわせてＣをつくり、
　何らかの素数Ｄが
　Ｃを割り切る
とせよ。

• 「数（について）・・・とせよ」は、 コメント４（命題７ー１）参照のこと。
• 　数Ａ、Ｂ
  に対して、
  　数Ｃ(;ｇ＝Ａ×Ｂ)、
  　素数Ｄ[;;｜Ｃ]
  をとっている。

　Ｄは
　Ａ、Ｂの１つを割り切る
と主張する。

• 　一方を割り切らない
  とすると
  　他方を割り切る
  　ことになるかどうかを
  　検証する。
  そこで
  　Ａを割り切らない場合と
  　Ｂを割り切らない場合とを
  　分ける。
  

　Ａを割り切らない
とせよ。
　　　　　　[......(ａ)]

• 場合分け（１）である。
  
• 　Ｄ;¬｜Ａ
  としている。

そして
　Ｄは素数である。

• 命題の設定による。
• 　Ｄ;素数
  となっている。

それゆえ
　Ａ、Ｄは互いに素である。
　　　　　　[......(１)]

• 命題７ー２９（素数は倍数以外に対して素）
  による。
  
• 　Ａ;(互いに素)Ｄ
  となっている。

そして
　ＤがＣを割った商に等しい 個数の単位が
　Ｅのなかにある
とせよ。
　　　　　　[......(a)]

• 命題の設定による。
• 　数Ｅ(;;個数(Ｅ,単位)＝商(Ｃ,Ｄ)＝ｅ)
  をとっている。

そうすれば
　ＤがＣを割った商は
　Ｅのなかにある単位の個数であるから、
　Ｄは
　ＥにかけてＣをつくった。

• 定義７ー８の補足（商）
  による。
  
• 　Ｄ;×Ｅ＝Ｃ
  となっている。

ところが
　Ａも
　ＢにかけてＣをつくった。

• 命題の設定による。
• 　Ａ;×Ｂ＝Ｃ
  となっている。

それゆえ
　Ｄ、Ｅの積は
　Ａ、Ｂの積に等しい。

• 公理の補足２（命題７ー４）（約数・等分(倍数)での代入の原理）
  による。
• 　Ｄ×Ｅ＝Ａ×Ｂ
  となっている。

ゆえに
　ＤがＡに対するように、
　ＢがＥに対する。

• 命題７ー１９（４数の比例と内項・外項の積）
  による。
• 　Ｄ：Ａ＝Ｂ：Ｅ
  となっている。

ところが
　Ａ、Ｄは
　互いに素であり、

• （１）による。
• 　Ａ;(互いに素)Ｄ
  となっている。

　【互いに】素である数は
　最小でもあり、

• 命題７ー２１（互いに素な数は同じ比の最小）
  による。
• 　(Ｄ：Ａ);(最小)
  となっている。

　最小の数は
　同じ比をもつ数を、
　大きい数は大きい数を、
　小さい数は小さい数を、
　すなわち
　前項は前項を、
　後項は後項を割り切り、
　その商は等しい。

• 命題７ー２０（同じ比なら最小のが割り切る）
  である。
• 　Ｄ;｜Ｂ、
  　Ａ;｜Ｅ
  となっている。

したがって
　ＤはＢを割り切る。

• 前節による。
• 　Ｄ;｜Ｂ
  となっている。

同様にして
もし
　Ｂを割り切らない
ならば、

• 場合分け（２） である。

　Ａを割り切る
であろうことを証明しうる。

• 　Ｄ;｜Ａ
  となっている。

よって
　［２つの場合の結果により］
　ＤはＡ、Ｂの１つを割り切る。

• 　Ｄ;｜(Ａ or Ｂ)
  となっている。

　これが証明すべきことであった。

• 命題７ー３０は、
  　数Ａ、Ｂ
  に対して、
  　素数Ｄ[;;｜Ａ×Ｂ]
  をとれば、
  　Ｄ;｜(Ａ or Ｂ)
  のことである。
  
• 命題７ー３０は推論用命題である。

  前提	作図	推論
  定義		7-8補
  公準
  公理		補2(題7-4)
  命題		7-19,7-20,7-21,7-29
  その他	コ4(題7-1)	場合分け

前 　　 次 　　 目次 　　頁頭