ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー２９（素数は倍数以外に対して素）
　すべて素数は
　それが割り切らないすべての数に対して素
　である。

• 素数は、 定義７ー１２による。
• 割り切るは、 定義５ー１の補足２による。
• 数は、 定義７ー２による。
• 対して素は、 定義の補足（命題７ー２３）による。

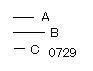
　Ａを素数
とし、
　ＡがＢを割り切らない
とせよ。

• 「数（について）・・・とせよ」は、 コメント４（命題７ー１） 参照のこと。
• 　素数は、
  　定義７ー１２（素数）
  により、
  　２、３、５、７、・・・
  と存在する。
  　無限に存在することは、
  　命題９ー２０（素数は無数）
  まで待たねばならない。
• 　素数Ａ
  に対して、
  　数Ｂ[;;Ａ¬｜Ｂ]
  をとっている。

　Ｂ、Ａは互いに素である
と主張する。

もし
　Ｂ、Ａが互いに素でない
ならば、

• 背理法の仮定を述べようとしている。

　何らかの数がそれらを割り切る
であろう。

　Ｃが割り切る
とせよ。

• 背理法の仮定である。
  
• 　Ｃ;｜(Ａ、Ｂ)
  としている。

　ＣはＢを割り切り、
　ＡはＢを割り切らない

• 命題の設定、 背理法の仮定 による。
• 　Ｃ;｜Ｂ、
  　Ａ;¬｜Ｂ
  となっている。

から、
　ＣはＡと同じではない。

• もし
  　ＣがＡと同じ
  なら、
  　背理法の仮定、
  　公理の補足２（命題７ー４）（約数・等分(倍数)での代入の原理）
  により、
  　ＡはＢを割り切り、
  　命題の設定
  　に矛盾する
  ので
  　ＣはＡと同じではない。
  
• 　Ｃ;≠Ａ
  となっている。

そして
　Ｂ、Ａを割り切る

• 背理法の仮定による。
• 　Ｃ;｜(Ｂ、Ａ)
  となっている。

から、
　素数であるＡを
　それと同じでない
のに
　割り切ることになる。

　これは不可能である。

• 定義７ー１２（素数）
  に矛盾する。

それゆえ
　いかなる数もＢ、Ａを割り切らない
であろう。

• 背理法による。

よって
　Ａ、Ｂは互いに素である。

• 　定義７ー１２（素数）
  による。
• 　Ａ;(互いに素)Ｂ
  となっている。

　これが証明すべきことであった。

• 命題７ー２９は、
  　素数Ａ
  に対して、
  　数Ｂ[;;Ａ¬｜Ｂ]
  をとれば、
  　Ａ;(互いに素)Ｂ
  のことである。
• 命題７ー２９は推論用命題である。

  前提	作図	推論
  定義		7-12
  公準
  公理		補2(題7-4)
  命題
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭