ユークリッド原論をどう読むか（８）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第４巻

命題４ー１１（作図.円に正５角形を内接）
等角２　 五角形　
与えられた円に
　等辺等角な五角形を内接させること。

• 円は、 定義１ー１５ による。
• 等辺は、 定義１ー２０の補足 による。
• 等角は、 定義１ー１９の補足２ にいう多角形において、
  　すべての角が等しいことをいう。
  （以下、定義の補足（命題４ー１１）(等角２)という。）
  定義の補足（命題４ー２） にいう等角とは
  　異なる概念である。
• 五角形は、角（辺）の数が５つの、 定義１ー１９の補足２ にいう多角形である。
  （以下、定義の補足２（命題４ー１１）(五角形)という。）
• 内接は、 定義４ー３ による。

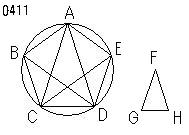
与えられた円を
　ＡＢＣＤＥとせよ。

• 　円ＡＢＣＤＥ
  をとっている。

このとき
　円ＡＢＣＤＥに
　等辺等角な五角形を内接させねばならぬ。

Ｇ、Ｈにおける角の双方が
　Ｆにおける角の２倍である
　　二等辺三角形ＦＧＨが
　定められ、 【・・・(a)】

• 命題４ー１０ （作図.角が1:2:2の二等辺三角形）
  による。
• 　線分ＦＧ
  をとり、
  　ＦＧ
  に対して、
  　二等辺三角形ＦＧＨ[;;∠Ｇ＝∠Ｈ＝２∠Ｆ]
  をとっている。

　 円ＡＢＣＤＥに
　三角形ＦＧＨに等角な
　　三角形ＡＣＤが
　内接され、
　角ＣＡＤが
　Ｆにおける角に等しくなるようにし、
　角ＡＣＤ、ＣＤＡの双方が
　Ｇ、Ｈにおける角の双方に
　等しくなるようにせよ。 【・・・(b)】

• 命題４ー２ （作図.等角三角形の内接）
  により、
  　等角な三角形が内接されたとき、
  　三角形の角をＡ、Ｃ、Ｄとし、
  　溯って用いている。
• 　円ＡＢＣＤＥ
  に対して、
  　△ＡＣＤ[;;（内接）円ＡＢＣＤＥ,（等角）△ＦＧＨ]
  をとっている。

そうすれば
角ＡＣＤ、ＣＤＡの双方は
　角ＣＡＤの２倍である。 【・・・(1)】

• (a) (b) による。
• 　∠ＡＣＤ＝∠ＣＤＡ＝２∠ＣＡＤ
  となっている。

そこで
　 角ＡＣＤ、ＣＤＡの双方が
　線分ＣＥ、ＤＢの双方によって
　２等分され、 【・・・(c)】

• 命題１ー９ （作図・角の２等分）
  により、
  　角ＡＣＤをＣＥで２等分する。
  ＣＥは
  　 命題３−２の補足 (円内通過直線は円周と２交点)
  により、
  　Ｃ以外に
  　円周と１点で交わる。
  ＣＥは
  　角ＡＣＤの内部にあるから、
  その交点は
  　弧ＡＤ上にあり、
  　その点をＥとして、
  　溯って用いている。
  Ｂについても同様である。
• 　交点Ｅ(二等分線(∠ＡＣＤ),円周ＡＢＣＤＥ)、
  　交点Ｂ(二等分線(∠ＡＤＣ),円周ＡＢＣＤＥ)
  をとっている。

　ＡＢ、ＢＣ、ＤＥ、ＥＡが結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 　線分ＡＢ、ＢＣ、ＤＥ、ＥＡ
  をとっている。

そうすれば
角ＡＣＤ、ＣＤＡの双方は
　角ＣＡＤの２倍であり、

• (1)による。
• 　∠ＡＣＤ＝∠ＣＤＡ＝２∠ＣＡＤ
  となっている。

　線分ＣＥ、ＤＢによって
　２等分されているから、

• (c)による。
• 　ＣＥ;二等分線(∠ＡＣＤ)、
  　ＤＢ;二等分線(∠ＡＤＣ)
  となっている。

５つの角ＤＡＣ、ＡＣＥ、ＥＣＤ、ＣＤＢ、ＢＤＡは
　互いに等しい。

• 公理１ー６ （同じものの半分）
  による。
• 　∠ＤＡＣ＝∠ＡＣＥ＝∠ＥＣＤ＝∠ＣＤＢ＝∠ＢＤＡ
  となっている。

ところが
等しい角は
　等しい弧の上に立つ。

• 命題３ー２６ （角が等しければ弧は等しい）
  による。

それゆえ
５つの弧ＡＢ、ＢＣ、ＣＤ、ＤＥ、ＥＡは
　互いに等しい。 【・・・(2)】

• 　弧ＡＢ＝弧ＢＣ＝弧ＣＤ＝弧ＤＥ＝弧ＥＡ
  となっている。

また
　等しい弧には等しい弦が対する。

• 命題３ー２９ （弧が等しければ弦も等しい）
  による。

それゆえ
５つの弦ＡＢ、ＢＣ、ＣＤ、ＤＥ、ＥＡは
　互いに等しい。

• 　弦ＡＢ＝弦ＢＣ＝弦ＣＤ＝弦ＤＥ＝弦ＥＡ
  となっている。

したがって
五角形ＡＢＣＤＥは
　等辺である。 【・・・(3)】

• 定義１ー２０の補足 （等辺）
  による。
• 　五角啓ＡＢＣＤＥ;等辺
  となっている。

次ぎに
　等角でもあると主張する。
弧ＡＢは
　弧ＤＥに等しいから、

• (2)による。
• 　弧ＡＢ＝弧ＤＥ
  となっている。

　双方に
　ＢＣＤが加えられたとせよ。
そうすれば
弧ＡＢＣＤ全体は
　弧ＥＤＣＢ全体に等しい。

• 公理１ー２ （等しいものに等しいものを加える）
  による。
• 　弧ＡＢＣＤ＝弧ＥＤＣＢ
  となっている。

そして
角ＡＥＤは
　弧ＡＢＣＤ上に立ち、
角ＢＡＥは
　弧ＥＤＣＢ上に立つ。
ゆえに
角ＢＡＥも
　角ＡＥＤに等しい。

• 命題３ー２７ （弧が等しければ角も等しい）
  による。
• 　∠ＢＡＥ＝∠ＡＥＤ
  となっている。

同じ理由で
角ＡＢＣ、ＢＣＤ、ＣＤＥのおのおのも
　角ＢＡＥ、ＡＥＤの双方に等しい。

• 　∠ＡＢＣ＝∠ＢＣＤ＝∠ＣＤＥ＝∠ＢＡＥ＝∠ＡＥＤ
  となっている。

したがって
五角形ＡＢＣＤＥは
　等角である。

• 定義の補足（命題４ー２） (等角)
  による。
• 　五角形ＡＢＣＤＥ;等角
  となっている。

ところが
　等辺であることも先に証明された。

• (3)による。
• 　五角形ＡＢＣＤＥ;等辺
  となっている。

よって
　与えられた円に
　等辺等角な五角形が内接された。
これが作図すべきものであった。

• 命題４ー１１は、
  　円ＡＢＣＤＥ
  に対して、
  　線分ＦＧ、
  　二等辺三角形ＦＧＨ[;;∠Ｇ＝∠Ｈ＝２∠Ｆ]、
  　△ＡＣＤ[;;（内接）円ＡＢＣＤＥ,（等角）△ＦＧＨ]
  　交点Ｅ(二等分線(∠ＡＣＤ),円周ＡＢＣＤＥ)、
  　交点Ｂ(二等分線(∠ＡＤＣ),円周ＡＢＣＤＥ)
  　線分ＡＢ、ＢＣ、ＤＥ、ＥＡ
  をとれば、
  　五角形ＡＢＣＤＥ;等辺、等角、（内接）円ＡＢＤＣＥ
  となっている。
  
• 命題４ー１１は作図用命題である。

  前提	作図	推論
  定義		1-20補,補(題4-2)
  公準	1-1
  公理		1-2,1-6
  命題	1-9 , 3-2補,4-2,4-10	3-26,3-27,3-29
  その他

前 　　 次 　　 目次 　　頁頭