ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー２６（角が等しければ弧は等しい）
等しい円において
　等しい角は、
　中心角も円周角も、
　等しい弧の上に立つ。

• 等しいは、 公理１ー７ による。
• 円は、 定義１ー１５ による。
• 角は、 定義１ー８ による。
• 中心角は、 定義の補足２（命題３ー２０） による。
• 円周角は、 定義の補足３（命題３ー２０） による。
• 弧は、 定義１ー１８の補足 による。

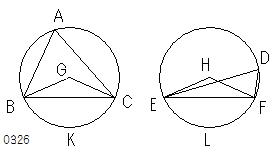
ＡＢＣ、ＤＥＦを等しい円とし、
　それらにおいて
　角ＢＧＣ、ＥＨＦを
　等しい中心角、
　角ＢＡＣ、ＥＤＦを
　等しい円周角とせよ。

• 　円ＡＢＣ
  に対して、
  　中心Ｇ.円ＡＢＣ、
  　点Ａ[上.円周ＡＢＣ]、
  　点Ｂ[上.円周ＡＢＣ,外.Ａ]、
  　点Ｃ[上.円周ＡＢＣ,外.Ａ,外.Ｂ]、
  　点Ｈ[]
  　円ＤＥＦ(Ｈ,ＧＢ)、
  　点Ｅ[上.円周ＤＥＦ]、
  　点Ｆ(上.円周ＤＥＦ,同向側(ＥＨ,ＢＧ,Ｃ);;∠ＥＨＦ＝∠ＢＧＣ)、
  　点Ｄ[上.円周ＤＥＦ,同向側(ＥＦ,ＢＣ,Ｄ);;∠ＢＡＣ＝∠ＥＤＦ]
  をとっている。

弧ＢＫＣは
　弧ＥＬＦに等しい
　と主張する。

ＢＣ、ＥＦが
　結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 　線分ＢＣ、ＥＦ
  をとっている。

そうすれば
円ＡＢＣ、ＤＥＦは
　等しいから、

• 命題の設定 による。
• 　円ＡＢＣ＝円ＤＥＦ
  となっている。

半径は
　等しい。

• 定義１ー１６の補足 （半径）
  による。

そこで
２線分ＢＧ、ＧＣは
　２線分ＥＨ、ＨＦに
　等しい。

• 公理１ー１の補足 （等しいものに等しい）
  による。
• 　(ＢＧ、ＧＣ)＝(ＥＨ,ＨＦ)
  となっている。

そして
Ｇにおける角は
　Ｈにおける角に等しい。

• 命題の設定 による。
• 　∠ＢＧＣ＝∠ＥＨＦ
  となっている。

それゆえ
底辺ＢＣは
　底辺ＥＦに等しい。 【・・・(1)】

• 命題１ー４ （２辺挟角相等）
  による。
• 　ＢＣ＝ＥＦ
  となっている。

そして
Ａにおける角は
　Ｄにおける角に等しいから、

• 命題の設定 による。
  命題３ー２０ （中心角は円周角の２倍）
  により、
  　一方が
  　　等しければ
  　他方も等しい。
• 　∠ＢＡＣ＝∠ＥＤＦ
  となっている。

切片ＢＡＣは
　切片ＥＤＦに相似である。

• 定義３ー１１ （相似な切片）
  による。
• 　切片ＢＡＣ∽切片ＥＤＦ
  となっている。

しかも
　等しい弦の上にある。

• (1) による。
• 　ＢＣ＝ＥＦ
  となっている。

ところが
　等しい弦の上にある、
　　円の相似な切片は
　互いに等しい。

• 命題３ー２４ （等しい線分の相似な切片は等しい）
  による。

ゆえに
切片ＢＡＣは
　ＥＤＦに等しい。

• 　切片ＢＡＣ≡切片ＥＤＦ
  となっている。

ところが
円ＡＢＣ全体も
　円ＤＥＦ全体に等しい。

• 命題の設定 による。
• 　円ＡＢＣ≡円ＤＥＦ
  となっている。

したがって
残りの弧ＢＫＣは
　弧ＥＬＦに等しい。

• 公理１ー７ （等しい）
  による。
• 　弧ＢＫＣ≡弧ＥＬＫ
  となっている。

よって
　等しい円において
等しい角は、
　中心角も円周角も、
　等しい弧の上に立つ。
これが証明すべきことであった。

• 命題３ー２６は、
  　円ＡＢＣ
  に対して、
  　円ＤＥＦ≡円ＡＢＣ、
  　中心角ＢＧＣ.円ＡＢＣ＝中心角ＥＨＦ.円ＤＥＦ、
  　円周角ＢＡＣ.円ＡＢＣ＝円周角ＥＤＦ.円ＤＥＦ
  をとれば、
  　弧ＢＣ≡弧ＥＦ
  のことである。
• 命題３ー２６は推論用命題である。

  前提	作図	推論
  定義		1-16補 ,3-11
  公準	1-1
  公理		1-1補 ,1-7
  命題		1-4 ,3-20 ,3-24
  その他

前 　　 次 　　 目次 　　頁頭