0410ユークリッド原論４

ユークリッド原論をどう読むか（８）
頁末　　前　　次　　目次

ユークリッド原論

第４巻

命題４ー１０（作図.角が1:2:2の二等辺三角形）
底辺における角の双方が
　残りの角の２倍である
　　二等辺三角形をつくること。

底辺は、 定義１ー２０の補足２ による。
角は、 定義１ー８ による。
倍は、 定義の補足（公理１ー５） による。
二等辺三角形は、 定義１ー２０ による。

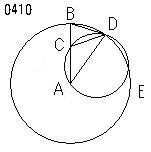
線分ＡＢがひかれ、

公準１ー１ （作図.直線）
による。
　線分ＡＢ
をとっている。

　点Ｃにおいて分けられ、
　ＡＢ、ＢＣにかこまれた矩形が
　ＣＡ上の正方形に等しくなる
　ようにせよ。 【・・・(a)】

命題２ー１１ （作図.線分の混合分割）
による。
　矩形(ＡＢ,ＢＣ)＝正方(_ＣＡ)
となっている。

Ａを中心とし、
　ＡＢを半径として
　円ＢＤＥが描かれ、

公準１ー３ （作図.円）
による。
　円ＢＤＥ(Ａ,ＡＢ)
をとっている。

　円ＢＤＥに
　円ＢＤＥの直径より大きくない
　　線分ＡＣに等しい
　線分ＢＤが挿入されたとせよ。 【・・・(b)】

命題４ー１ （作図.線分の挿入）
による。
挿入の一方の端が
　Ｂとなるようにして、
　他方の端をＤとする。
ＡＢが半径であり、
ＡＣは
　その部分であるから、
　 公理１ー８ （大きい）
により
　直径より小さい。
　点Ｄ[上.円周ＢＤＥ;;ＢＤ＝ＡＣ]
をとっている。

そして、
　ＡＤ、ＤＣが結ばれ、

公準１ー１ （作図.直線）
による。
　線分ＡＤ、ＤＣ
をとっている。

　三角形ＡＣＤに
　円ＡＣＤが外接されたとせよ。 【・・・(c)】

命題４ー５ （作図.三角形の外接円）
による。
　円ＡＣＤ[;;円ＡＣＤ（外接）△ＡＣＤ]
をとっている。

そうすれば、
矩形ＡＢ、ＢＣは
　ＡＣ上の正方形に等しく、

(a)による。
　矩形(ＡＢ,ＢＣ)＝正方(_ＡＣ)
となっている。

ＡＣは
　ＢＤに等しいから、

(b)による。
　ＡＣ＝ＢＤ
となっている。

矩形ＡＢ、ＢＣは
　ＢＤ上の正方形に等しい。 【・・・(1)】

定義１ー２２ （正方形・矩形・菱形・長斜方形・トラペジオン）、
公理１ー１ （同じものに等しい）
による。
　矩形(ＡＢ,ＢＣ)＝正方(_ＢＤ)
となっている。

そして
　円ＡＣＤの外部に
　任意の点Ｂがとられ、

Ｂは
　最初から設定されている。
次ぎにあげる
　命題の立場から論じている。
　Ｂ;外.円ＡＣＤ
となっている。

　Ｂから円ＡＣＤに
　２線分ＢＡ、ＢＤがひかれ、

すでに、(a)(b)でひかれている。

　それらの一方が円を切り、
　他方が円周上におち、

(c)により、
線分ＡＢは
　円ＡＣＤをきる。
ＢＤは
　端点Ｄが円周上にあることによる。
　ＢＡ;（切）円ＡＣＤ、
　Ｄ;上.円周ＡＣＤ
となっている。

矩形ＡＢ、ＢＣは
　ＢＤ上の正方形に等しいから、

(1)による。
　矩形(ＡＢ,ＢＣ)＝正方(_ＢＤ)
となっている。

ＢＤは
　円ＡＣＤに接する。

命題３ー３７ （いわゆる方べきの定理の逆）
による。
　ＢＤ（接）円ＡＣＤ
となっている。

そこで
　ＢＤが接し、
　ＤＣが接点Ｄからひかれたから、
角ＢＤＣは
　円の反対側の切片内の角ＤＡＣに等しい。

命題３ー３２ （いわゆる接弦定理）
による。
　∠ＢＤＣ＝∠ＤＡＣ
となっている。

そこで
角ＢＤＣは
　角ＤＡＣに等しいから、
　双方に角ＣＤＡが加えられたとせよ。
そうすれば
角ＢＤＡ全体は
　２角ＣＤＡ、ＤＡＣの和に等しい。

公理１ー２ （等しいものに等しいものを加える）
による。
　∠ＢＤＡ＝∠ＣＤＡ＋∠ＤＡＣ
となっている。

ところが
外角ＢＣＤは
　角ＣＤＡ、ＤＡＣの和に等しい。

命題１ー３２ （三角形の内対角・内角の和）
による。
　∠ＢＣＤ＝∠ＣＤＡ＋∠ＤＡＣ
となっている。

ゆえに
　角ＢＤＡも角ＢＣＤに等しい。

公理１ー１ （同じものに等しい）
による。
　∠ＢＤＡ＝∠ＢＣＤ
となっている。

また、
ＡＤは
　ＡＢに等しいから、

(b) 定義１ー１５ （円）
による。
　ＡＤ＝ＡＢ
となっている。

角ＢＤＡは
　角ＣＢＤに等しい。

命題１ー５ （２等辺三角形の底角）
による。
　∠ＢＤＡ＝∠ＣＢＤ
となっている。

したがって
　角ＤＢＡも角ＢＣＤに等しい。

公理１ー１ （同じものに等しい）
による。
　∠ＤＢＡ＝∠ＢＣＤ
となっている。

それゆえ
３つの角ＢＤＡ、ＤＢＡ、ＢＣＤは
　互いに等しい。 【・・・(2)】

　∠ＢＤＡ＝∠ＤＢＡ＝∠ＢＣＤ
となっている。

そして、
角ＤＢＣは
　角ＢＣＤに等しいから、
辺ＢＤも
　辺ＤＣに等しい。

命題１ー６ （等しい底角なら二等辺三角形）
による。
　ＢＤ＝ＤＣ
となっている。

ところが
ＢＤは
　ＣＡに等しい
　と仮定されている。

(b)による。
　ＢＤ＝ＣＡ
となっている。

ゆえに
　ＣＡもＣＤに等しい。

公理１ー１ （同じものに等しい）
による。
　ＣＡ＝ＣＤ
となっている。

したがって
　角ＣＤＡも角ＤＡＣに等しい。

命題１ー５ （２等辺三角形の底角）
による。
　∠ＣＤＡ＝∠ＤＡＣ
となっている。

それゆえ
角ＣＤＡ、ＤＡＣの和は
　角ＤＡＣの２倍である。

定義の補足（公理１ー５） （同じもののｎ倍）
による。
　∠ＣＤＡ＋∠ＤＡＣ＝２∠ＤＡＣ
となっている。

そして
角ＢＣＤは
　角ＣＤＡ、ＤＡＣの和に等しい。

命題１ー３２ （三角形の内対角・内角の和）
による。
　∠ＢＣＤ＝∠ＣＤＡ＋∠ＤＡＣ
となっている。

ゆえに
　角ＢＣＤも角ＣＡＤの２倍である。

公理１ー１ （同じものに等しい）
による。
　∠ＢＣＤ＝２∠ＣＡＤ
となっている。

ところが
角ＢＣＤは
　角ＢＤＡ、ＤＢＡの双方に等しい。

(2) による。
　∠ＢＣＤ＝∠ＢＤＡ＝∠ＤＢＡ
となっている。

したがって
角ＢＤＡ、ＤＢＡの双方は
　角ＤＡＢの２倍である。

公理１ー１（同じものに等しい）
による。
　∠ＢＤＡ＝∠ＤＢＡ＝２∠ＤＡＢ
となっている。

よって
　底辺ＤＢにおける角の双方が
　残りの角の２倍である
　　二等辺三角形ＡＢＤがつくられた。
これが作図すべきものであった。

命題４ー１０は、
　線分ＡＢ、
　点Ｃ(ＡＢ;;矩形(ＡＢ,ＢＣ)＝正方(_ＣＡ))、
　円ＢＤＥ(Ａ,ＡＢ)、
　点Ｄ[上.円周ＢＤＥ;;ＢＤ＝ＡＣ]、
　線分ＡＤ
をとれば、
　△ＡＢＤ;２等辺三角形(;;ＡＢ＝ＡＤ,∠ＡＢＤ＝∠ＡＤＢ＝２∠ＢＡＤ)
のことである。
命題４ー１０は作図用命題である。

前提作図推論
定義 1-15,1-22,補(理1-5)
公準 1-1,1-3
公理 1-1,1-2,1-8
命題 2-11,4-1,4-5 1-5,1-6,1-32,3-32,3-37
その他

前　　次　　目次　　頁頭

前提	作図	推論
定義		1-15,1-22,補(理1-5)
公準	1-1,1-3
公理		1-1,1-2,1-8
命題	2-11,4-1,4-5	1-5,1-6,1-32,3-32,3-37
その他