ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー３２（いわゆる接弦定理）
もし
　円に直線が接し、
　その接点から
　円に対し円を切る直線が
　ひかれるならば、
　それが
　　接線となす角は
　円の
　反対側の切片内の角に
　等しいであろう。

• 円は、 定義１ー１５ による。
• 直線は、 定義１ー４ による。
• 接するは、 定義３ー２ による。
• 接点は、 定義３ー２の補足３ による。
• 切るは、 定義３ー２の補足２ による。
• 接線は、 定義３ー２の補足３ による。
• 角は、 定義１ー８ による。
• 反対側は、 定義１ー７の補足 による。弦と接線とがなす角の反対側、すなわち弦について、角をなす半直線と反対側にあるということである。
• 切片内の角は、 定義３ー８ による。
• 等しいは、 公理１ー７ による。

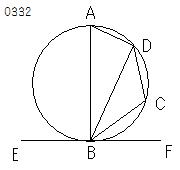
直線ＥＦが
　円ＡＢＣＤに
　点Ｂにおいて接するとし、
　点Ｂから
　円ＡＢＣＤに
　それを切る直線ＢＤが
　ひかれたとせよ。

• 公準１ー１の補足 （作図.任意の点をとる）
  により、
  　円周上の
  　Ｂ以外のところに
  　Ｄをとる。
  公準１ー１ （作図.直線）
  により
  　ＢとＤとを結ぶと
  直線ＢＤは、
  　 定義３ー２の補足２ （切る）
  により
  　円を切る。
• 　円ＡＢＣＤ
  に対して、
  　直線ＥＦ[;;（接）円ＡＢＣＤ]、
  　接点Ｂ(直線ＥＦ,円ＡＢＣＤ)、
  　点Ｄ[円ＡＢＣＤ,外.Ｂ]、
  をとっている。

ＢＤが
　接線ＥＦとなす角は
　円の
　反対側の切片内の角に
　等しいであろう。
すなわち
ＦＢＤは
　切片ＢＡＤ内につくられた角に
　等しく、
角ＥＢＤは
　切片ＤＣＢ内につくられた角に
　等しい
　と主張する。

Ｂから
　ＥＦに直角に
　ＢＡがひかれたとし、 【・・・(a)】

• 命題１ー１１ （作図・線分からの垂線）
  により、
  直角にひかれた直線は、
  　 命題３ー１９ （中心は接線の接点からの垂線上）
  により、
  　その上に中心があるので、
  　 命題３−１の補足２ (中心を通る直線は円周と２交点)
  により、
  　円周と
  　Ｂ以外にもう１つの交点Ａをもつ。
  Ａが
  　角ＡＢＦの内部に
  　　Ｄがある場合と
  　角ＡＢＦの外部に
  　　Ｄがある場合と
  　Ｄと一致する場合と
  　がある。
  
• 　交点Ａ(垂線(Ｂ,ＥＦ),円周ＡＢＣＤ)
  をとっている。

［ 角ＡＢＦの内部にＤがある場合は、 ］

• 　Ｄ;同側(ＡＢ,Ｆ)∩同側(ＢＦ,Ａ)
  となっている。

　弧ＢＤ上に
　任意の点Ｃがとられ、

• 公準１ー１の補足 （作図.任意の点をとる）
  による。
• 　点Ｃ[内.弧ＢＤ]
  をとっている。

　ＡＤ、ＤＣ、ＣＢが
　結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 　線分ＡＤ、ＤＣ、ＣＢ
  をとっている。

そうすれば
直線ＥＦは
　円ＡＢＣＤにＢにおいて接し、

• 命題の設定 による。
• 　ＥＦ（接）円ＡＢＣＤ
  となっている。

　接点から
　接線に直角に
　ＢＡがひかれたから、

• (a) による。
• 　ＢＡ⊥ＥＦ
  となっている。

円ＡＢＣＤの中心は
　ＢＡ上にある。

• 命題３ー１９ （中心は接線の接点からの垂線上）
  による。
• 　中心.円ＡＢＣＤ;上.ＢＡ
  となっている。

それゆえ
ＢＡは
　円ＡＢＣＤの直径である。

• 定義１ー１７ （直径）
  による。
• 　線分ＢＡ;直径.円ＡＢＣＤ
  となっている。

ゆえに
角ＡＤＢは
　半円内にあるから
　直角である。

• 命題３ー３１ （半円内の角は直角、半円より大小の切片内の角、切片の角）、
  による。
• 　∠ＡＤＢ＝∠Ｒ
  となっている。

したがって
残りの角ＢＡＤ、ＡＢＤの和は
　直角に等しい。

• 命題１ー３２ （三角形の内対角・内角の和）、
  公理１ー３ （等しいものから等しいものをひく）
  による。
• 　∠ＢＡＤ＋∠ＡＢＤ＝∠Ｒ
  となっている。

ところが
角ＡＢＦも
　直角である。

• (a) による。
• 　∠ＡＢＦ＝∠Ｒ
  となっている。

それゆえ
角ＡＢＦは
　角ＢＡＤ、ＡＢＤの和に等しい。

• 公理１ー１ （同じものに等しい）
  による。
• 　∠ＡＢＦ＝∠ＢＡＤ＋∠ＡＢＤ
  となっている。

双方から
角ＡＢＤが
　ひかれたとせよ。
そうすれば
残りの角ＤＢＦは
　円の
　反対側の切片内の角ＢＡＤに
　等しい。 【・・・(1)】

• 公理１ー３ （等しいものから等しいものをひく）
  による。
  なお、
  　切片ＢＡＤ内の角は、
  　弧ＢＡＤのどこにあっても、
  　 命題３ー２１ （切片内の角は等しい）
  により等しい。
• 　∠ＤＢＦ＝∠ＢＡＤ
  となっている。

そして
ＡＢＣＤは
　円に内接する四辺形であるから、

• 定義の補足（命題３ー２２） (内接)
  による。
• 　四辺形ＡＢＣＤ;（内接）円ＡＢＣＤ
  となっている。

その対角の和は
　２直角に等しい。

• 命題３ー２２ （内接四辺形の対角の和は２直角）
  による。

ところが
角ＤＢＦ、ＤＢＥの和も
　２直角に等しい。

• 定義１ー１０ （直角）
  による。
• 　∠ＤＢＦ＋∠ＤＢＥ＝２∠Ｒ
  となっている。

それゆえ
角ＤＢＦ、ＤＢＥの和は
　角ＢＡＤ、ＢＣＤの和に等しく、

• 公理１ー１ （同じものに等しい）
  による。
• 　∠ＤＢＦ＋∠ＤＢＥ＝∠ＢＡＤ＋∠ＢＣＤ
  となっている。

そのうち
角ＢＡＤは
　角ＤＢＦに等しい
　ことが証明された。

• (1) による。
• 　∠ＢＡＤ＝∠ＤＢＦ
  となっている。

ゆえに
残りの角ＤＢＥは
　円の
　反対側の切片ＤＣＢ内の角ＤＣＢに等しい。

• 公理１ー３ （等しいものから等しいものをひく）
  による。
• 　∠ＤＢＥ＝∠ＤＣＢ
  となっている。

［ 角ＡＢＦの外部にＤがある場合は、

　ＥとＦの記号を付け替えればよい。
ＡとＤが一致する場合は、

　 命題３ー３１ （半円内の角は直角、半円より大小の切片内の角、切片の角）
により
　半円内の角が直角であり、
角ＤＢＦ、ＤＢＥは、
　直角であるから、
　円の反対側の切片内の、
　すなわち半円内の角に等しい。

したがって、
　３つの場合の結果により
　角ＤＢＦは、
　円の反対側の
　切片内の角に等しい。］

よってもし
　円に直線が接し、
　その接点から
　円に対して
　円を切る直線がひかれるならば、
それが接線となす角は
　円の
　反対側の切片内の角に
　等しいであろう。
これが証明すべきことであった。

• 命題３ー３２は、 　円ＡＢＣＤ
  に対して、
  　直線ＥＦ[;;（接）円ＡＢＣＤ]、
  　接点Ｂ(直線ＥＦ,円ＡＢＣＤ)、
  　点Ｄ[円ＡＢＣＤ,外.Ｂ]、
  　点Ａ'[円ＡＢＣＤ,内.反対側(ＢＤ,Ｆ)]、
  　点Ｃ[円ＡＢＣＤ,内.同側(ＢＤ,Ｆ)]
  　線分Ａ'Ｄ、ＤＣ、ＣＢ
  をとれば、
  　∠ＤＢＦ＝∠ＤＡ'Ｂ
  　∠ＤＢＥ＝∠ＤＣＢ
  のことである。
  
• 命題３ー３２は推論用命題である。

  前提	作図	推論
  定義		1-10,1-17,3-2補2,補(題3-22)
  公準	1-1,1-1補
  公理		1-1,1-3
  命題	1-11,3-1補2	1-32,3-19,3-21,3-22,3-31
  その他		場合分け

前 　　 次 　　 目次 　　頁頭