ユークリッド原論をどう読むか（１）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー６（等しい底角なら二等辺三角形）
もし
　三角形の２角が互いに等しけれ
ば、
　等しい角に対する辺も互いに等しい
であろう。

• 　三角形は定義１ー１９の補足２による。
• 　角は定義１ー８による。
• 　等しいは公理１ー７による。
• 　辺は定義１ー１９の補足による。

　ＡＢＣを
　角ＡＢＣが角ＡＣＢに等しい
とせよ。

• 　線分(Ｂ,Ｃ)、
  　点Ａ'(外.線分ＢＣ;;∠Ａ'ＢＣ＜∠Ｒ)、
  　点Ａ"(同側(ＢＣ,Ａ')
  　　　;;∠Ａ"ＣＢ＝∠Ａ'ＢＣ)、
  　交点Ａ(ＢＡ',ＣＡ")
  をとる。
  ただし、
  　∠Ａ'ＢＣに等しく
  　∠Ａ"ＣＢをとる
  のは、
  　仮想的である。
  　実際に可能となる
  のは、
  　命題１ー２３（作図・直線上に指定された角）
  まで待たねばならない。
  
• 　△ＡＢＣ;(∠ＡＢＣ＝∠ＡＣＢ)
  となっている。

　辺ＡＢも辺ＡＣに等しい
と主張する。

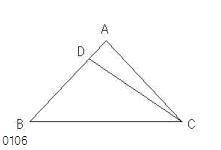
もし
　ＡＢが
　ＡＣに等しくない
ならば、

• 背理法の仮定である。

　そのうち一方は大きい。

• 　公理１ー７の補足（線分・角は大か等か小）
  による。

　ＡＢが大きい
とし、
　大きい方ＡＢから
　小さい方ＡＣに等しいＤＢが
　切り取られ[点Ｄが取られ]、

• 　命題１ー３（作図・等しい線分を切り取る）
  による。
• 　ＡＢ＞ＡＣ
  とし、
  　点Ｄ(ＡＢ;;ＤＢ＝ＡＣ)
  となっている。

　ＤＣが結ばれた
とせよ。
　　　　　　【・・・(a)】

• 　公準１ー１（作図.直線）
  による。
• 　線分(Ｄ,Ｃ)
  をとっている。

そうすれば
　ＤＢはＡＣに等しく、

• 　(a) による。
• 　ＤＢ＝ＡＣ
  となっている。

　ＢＣが共通である
から、
　２辺ＤＢ、ＢＣは
　２辺ＡＣ、ＣＢにそれぞれ等しく、
　角ＤＢＣは角ＡＣＢに等しい。

• 　前節、
  　命題の仮定
  による。
• 　(ＤＢ,ＢＣ)＝(ＡＣ,ＣＢ)、
  　∠ＤＢＣ＝∠ＡＣＢ
  となっている。

したがって
　底辺ＤＣは底辺ＡＢに等しく、
　三角形ＤＢＣは三角形ＡＣＢに等しく、

• 　前節、
  　命題１ー４（２辺挟角相等）
  による。
• 　合同という概念が
  　原論の世界では未成立である
  ことを示している。
• 　ＤＣ＝ＡＢ、
  　△ＤＢＣ≡△ＡＣＢ
  となっている。

　小さいものが
　大きいものに等しくなる
であろう。

• 　ＤはＡＢ上にある
  から、
  　三角形ＡＣＢは
  　ＤＢＣより大きい
  という意味である。
• 　△ＡＣＢ＞△ＤＢＣ
  かつ、
  　△ＡＣＢ≡△ＤＢＣ
  となっている。

　これは不合理である。

• 　角ＤＣＢが角ＡＢＣと等しく、
  　角ＡＢＣが角ＡＣＢと等しかった
  から、
  　角ＤＣＢが角ＡＣＢと等しく
  なる。
  　角ＤＣＢは角ＡＣＢより
  　明らかに小さい
  ので
  　不合理である
  と推論することもできる。

それゆえ
　ＡＢはＡＣに不等ではない。

• 　背理法による。

ゆえに
　等しい。

よって
もし
　三角形の２角が互いに等しけれ
ば、
　等しい角に対する辺も互いに等しい
であろう。

　これが証明すべきことであった。

• 　命題１ー５（２等辺三角形の底角）
  の逆である。
• 　命題の結論それ自体を否定して、
  　背理法で証明しているのは、
  　これが最初である。
  
  　背理法の活用は
  　命題１ー４（２辺挟角相等）の論証過程で
  　すでに登場している。
• 　命題1-6は、
  　△ＡＢＣ
  において、
  　∠ＡＢＣ＝∠ＡＣＢ
  ならば、
  　ＡＢ＝ＡＣ
  のことである。
  
• 　命題1-6は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理		1-7補
  命題	1-3	1-4
  その他		背理法

前 　　 次 　　 目次 　　頁頭