ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー３４（与えられた直線角を含む切片の切取）
与えられた円から
　与えられた直線角に
　等しい角を含む
　切片を切り取ること。

• 円は、 定義１ー１５ による。
• 直線角は、 定義１ー９ による。
• 等しいは、 公理１ー７ による。
• 角は、 定義１ー９ による。
• 含むは、 定義３ー１１の補足 による。
• 切片は、 定義３ー６ による。
• 切るは、 定義３ー２の補足２ による。

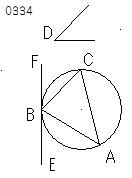
与えられた円をＡＢＣとし、
　与えられた直線角を角Ｄとせよ。

• 　円ＡＢＣ、
  　∠Ｄ
  をとっている。

このとき
　円ＡＢＣから
　与えられた直線角Ｄに
　等しい角を含む
　切片を切り取らねばならぬ。

点Ｂにおいて
　ＡＢＣに接する
　ＥＦがひかれ、

• 命題３ー１ （作図.円の中心）
  により、
  　円の中心が取られ、
  　 公準１ー１ （作図.直線）
  により
  　中心とＢとが結ばれ、
  　 命題１ー１１ （作図・線分からの垂線）
  により
  　Ｂから
  　この直線に直角に
  　半直線ＢＥをひき、
  　この半直線を
  　Ｂの方向に延長して接線ＥＦとする。
• 　垂線ＢＥ(Ｂ,線分(Ｂ,中心.円ＡＢＣ))、
  　点Ｆ(延長ＥＢ)、
  　直線ＥＦ
  をとれば、
  　ＥＦ(接)円ＡＢＣ
  となっている。

　直線ＦＢ上に
　その上の点Ｂにおいて
　角Ｄに等しい角ＦＢＣが
　つくられたとせよ。 【・・・(a)】

• 命題１ー２３ （作図・直線上に指定された角）
  による。
• 　∠ＦＢＣ[Ｂ,ＢＦ,∠Ｄ]
  をとっている。

そうすれば
直線ＥＦは
　円ＡＢＣに接し、
　接点Ｂから
　ＢＣがひかれたから、

• 　ＥＦ(接)円ＡＢＣ、
  　ＢＣ;(通)接点Ｂ
  となっている。

角ＦＢＣは
　反対側の
　切片ＢＡＣ内の角に等しい。

• 命題３ー３２ （いわゆる接弦定理）
  による。
• 　∠ＦＢＣ＝内角.切片ＢＡＣ(ＢＣ,円ＡＢＣ;;反対側(ＢＣ,Ｆ))
  となっている。

ところが
角ＦＢＣは
　角Ｄに等しい。

• (a) による。
• 　∠ＦＢＣ＝∠Ｄ
  となっている。

それゆえ
切片ＢＡＣ内の角も
　角Ｄに等しい。

• 公理１ー１ （同じものに等しい）
  による。
• 　内角.切片ＢＡＣ＝∠Ｄ
  となっている。

よって
　与えられた円ＡＢＣから
　与えられた直線角Ｄに等しい角を含む
　切片ＢＡＣが切り取られた。
これが作図すべきものであった。

• 命題３ー３４は、
  　円ＡＢＣ、∠Ｄ
  に対して、
  　点Ｂ[円周ＡＢＣ]、
  　垂線ＢＥ(Ｂ,線分(Ｂ,中心.円ＡＢＣ))、
  　点Ｆ(延長ＥＢ)、
  　∠ＦＢＣ[Ｂ,線分ＢＦ,∠Ｄ;;Ｃ;上.円周ＡＢＣ]、
  　切片ＢＡＣ(ＢＣ,円ＡＢＣ;;反対側(ＢＣ,Ｆ))
  をとれば、
  　内角.切片ＢＡＣ＝∠Ｄ
  のことである。
• 命題３ー３４は作図用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理		1-1
  命題	1-11,1-23,3-1	3-32
  その他

前 　　 次 　　 目次 　　頁頭