ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー２１（切片内の角は等しい）
円において
　同じ切片内の角は
　互いに等しい。

• 円は、定義１ー１５ による。
• 切片内の角は、定義３ー８ による。
• 等しいは、公理１ー７ による。

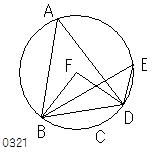
ＡＢＣＤを円とし、
　ＢＡＤ、ＢＥＤを
　同じ切片ＢＡＥＤ内の角とせよ。

• 　円ＡＢＣＤ
  に対して、
  　点Ｂ[円周ＡＢＣＤ]、
  　点Ｄ[円周ＡＢＣＤ,外.Ｂ]、
  　点Ａ[内.弧ＢＤ]、
  　点Ｃ[内.弧ＢＤ,反対側(ＢＤ,Ａ)]、
  　点Ｅ[内.弧ＢＤ,同側(ＢＤ,Ａ),外Ａ]
  をとっている。

角ＢＡＤ、ＢＥＤは
　互いに等しい
　と主張する。

円ＡＢＣＤの中心がとられ、
　それをＦとし、 【・・・(a)】

• 命題３ー１（作図.円の中心）
  による。
• 中心Ｆ.円ＡＢＣＤ
  をとっている。

　ＢＦ、ＦＤが結ばれたとせよ。

• 公準１ー１（作図.直線）
  による。
• 　線分ＢＦ、ＦＤ
  をとっている。

そうすれば
角ＢＦＤは
　中心角であり、

• (a) ,定義の補足２（命題３ー２０）(中心角)
  による。
• 　∠ＢＦＤ;中心角.円ＡＢＣＤ
  となっている。

角ＢＡＤは
　円周角であり、

• 定義の補足３（命題３ー２０）(円周角)
  による。
• 　∠ＢＡＤ;円周角.円ＡＢＣＤ
  となっている。

それらは
　同じ弧ＢＣＤを底辺とするから、
角ＢＦＤは
　角ＢＡＤの２倍である。

• 命題３ー２０（中心角は円周角の２倍）
  による。
• 　∠ＢＦＤ＝２∠ＢＡＤ
  となっている。

同じ理由で
角ＢＦＤは
　また
　角ＢＥＤの２倍である。

• 命題３ー２０（中心角は円周角の２倍）
  による。
• 　∠ＢＦＤ＝２∠ＢＥＤ
  となっている。

それゆえ
角ＢＡＤは
　角ＢＥＤに等しい。

• 公理１ー６（同じものの半分）
  による。
• 　∠ＢＡＤ＝∠ＢＥＤ
  となっている。

よって
　円において
　同じ切片内の角は
　互いに等しい。
これが
　証明すべきことであった。

• 今日的には、円周角は等しいという。
• 命題３ー２１は、
  　円ＡＢＣＤ
  に対して、
  　切片ＢＡＥＤ..円ＡＢＣＤ[]、
  　内角ＢＡＤ..切片ＢＡＥＤ[]、
  　内角ＢＥＤ..切片ＢＡＥＤ[]、
  をとれば、
  　∠ＢＡＤ＝ＢＥＤ
  のことである。
  
• 命題３ー２１は推論用命題である。

  前提	作図	推論
  定義		補2(題3-20) ,補3(題3-20)
  公準	1-1
  公理		1-6
  命題	3-1	3-20
  その他

前 　　 次 　　 目次 　　頁頭